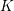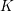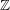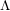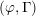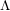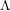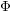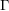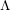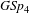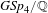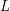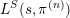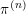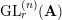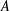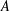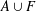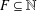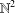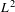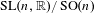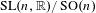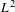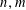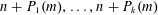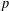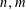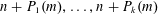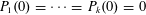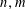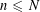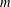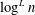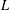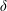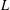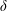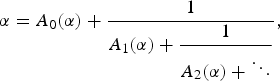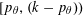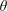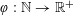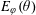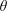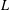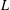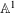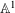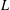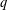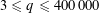Refine listing
Actions for selected content:
2816 results in 11xxx
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation
Pair correlation for quadratic polynomials mod 1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 960-983
- Print publication:
- May 2018
-
- Article
- Export citation
Approximation forte pour les variétés avec une action d’un groupe linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 773-819
- Print publication:
- April 2018
-
- Article
- Export citation
Cycles in the de Rham cohomology of abelian varieties over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 850-882
- Print publication:
- April 2018
-
- Article
- Export citation
Irreducibility of polynomials over global fields is diophantine
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 761-772
- Print publication:
- April 2018
-
- Article
- Export citation
The geometry of Hida families II:
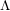 $\unicode[STIX]{x1D6EC}$ -adic
$\unicode[STIX]{x1D6EC}$ -adic 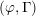 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and 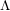 $\unicode[STIX]{x1D6EC}$ -adic Hodge theory
$\unicode[STIX]{x1D6EC}$ -adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 719-760
- Print publication:
- April 2018
-
- Article
- Export citation
VISIBLE POINTS ON EXPONENTIAL CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 353-359
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR
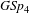 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 February 2018, pp. 351-419
- Print publication:
- March 2020
-
- Article
- Export citation
Generating functions on covering groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 671-684
- Print publication:
- April 2018
-
- Article
- Export citation
FINITELY STABLE ADDITIVE BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 360-362
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation
A Note on Rényi's ‘Record’ Problem and Engel's Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 363-369
-
- Article
- Export citation
APPROXIMATION OF
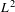 $L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE
$L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE 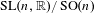 $\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 February 2018, pp. 307-350
- Print publication:
- March 2020
-
- Article
- Export citation
POLYNOMIAL PATTERNS IN THE PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 6 / 2018
- Published online by Cambridge University Press:
- 12 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 283-293
-
- Article
-
- You have access
- Open access
- Export citation
VARIANTS OF ERDŐS–SELFRIDGE SUPERELLIPTIC CURVES AND THEIR RATIONAL POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 380-386
- Print publication:
- 2018
-
- Article
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 184-210
- Print publication:
- 2018
-
- Article
- Export citation
RIGID LOCAL SYSTEMS ON
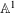 $\mathbb{A}^{1}$ WITH FINITE MONODROMY
$\mathbb{A}^{1}$ WITH FINITE MONODROMY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 785-846
- Print publication:
- 2018
-
- Article
- Export citation
EXPLICIT ZERO-FREE REGIONS FOR DIRICHLET
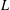 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 445-474
- Print publication:
- 2018
-
- Article
- Export citation