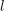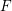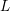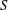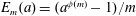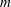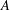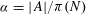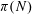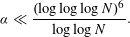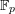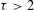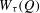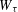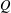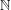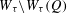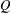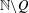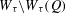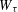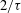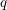Refine listing
Actions for selected content:
2818 results in 11xxx
Automorphy and irreducibility of some l-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 207-229
- Print publication:
- February 2015
-
- Article
- Export citation
Unnormalized differences between zeros of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 230-252
- Print publication:
- February 2015
-
- Article
- Export citation
FROM KHINCHIN’S CONJECTURE ON STRONG UNIFORMITY TO SUPERUNIFORM MOTIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 20 October 2014, pp. 591-707
- Print publication:
- September 2015
-
- Article
- Export citation
HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL
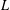 $L$-VALUES
$L$-VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 1-38
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON EXPONENTIAL DIOPHANTINE EQUATIONS CONTAINING THE EULER QUOTIENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 11-18
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
SINGLE-VALUED MOTIVIC PERIODS AND MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 October 2014, e25
-
- Article
-
- You have access
- Open access
- Export citation
ON IMPROVING ROTH’S THEOREM IN THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 49-62
- Print publication:
- January 2015
-
- Article
- Export citation
A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 41-46
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Galois representations attached to moments of Kloosterman sums and conjectures of Evans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 October 2014, pp. 68-120
- Print publication:
- January 2015
-
- Article
- Export citation
Computation on elliptic curves with complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 October 2014, pp. 509-535
-
- Article
-
- You have access
- Export citation
HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 101-120
- Print publication:
- January 2015
-
- Article
- Export citation
Unitary cycles on Shimura curves and the Shimura lift II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 1963-2002
- Print publication:
- December 2014
-
- Article
- Export citation
A NOTE ON INHOMOGENEOUS DIOPHANTINE APPROXIMATION IN BETA-DYNAMICAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 34-40
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
On fields of rationality for automorphic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 11 September 2014, pp. 2003-2053
- Print publication:
- December 2014
-
- Article
- Export citation
The Hardy–Littlewood conjecture and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 2095-2111
- Print publication:
- December 2014
-
- Article
- Export citation
THE TOTAL DISTANCE FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On families of 7- and 11-congruent elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 536-564
-
- Article
-
- You have access
- Export citation
Numerical calculation of three-point branched covers of the projective line
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 379-430
-
- Article
-
- You have access
- Export citation
Explicit Kummer varieties of hyperelliptic Jacobian threefolds
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 496-508
-
- Article
-
- You have access
- Export citation
Refined abelian Stark conjectures and the equivariant leading term conjecture of Burns
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1809-1835
- Print publication:
- November 2014
-
- Article
- Export citation