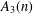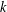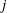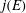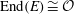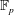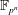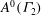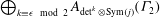Refine listing
Actions for selected content:
2818 results in 11xxx
Linear independence of monomials of multizeta values in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1789-1808
- Print publication:
- November 2014
-
- Article
- Export citation
The real Chevalley involution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 2127-2142
- Print publication:
- December 2014
-
- Article
- Export citation
INFINITE FAMILIES OF CONGRUENCES MODULO 3 AND 9 FOR BIPARTITIONS WITH 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 August 2014, pp. 47-52
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON WITTEN MULTIPLE ZETA-FUNCTIONS ASSOCIATED WITH SEMI-SIMPLE LIE ALGEBRAS V
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 107-130
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
THE DISTRIBUTION OF
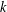 $k$ -TUPLES OF REDUCED RESIDUES
$k$ -TUPLES OF REDUCED RESIDUES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 72-88
- Print publication:
- January 2015
-
- Article
- Export citation
MATRIX PROGRESSIONS IN MULTIDIMENSIONAL SETS OF INTEGERS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 14-48
- Print publication:
- January 2015
-
- Article
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
COMPARING
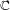 $\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
$\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 04 August 2014, pp. 71-84
- Print publication:
- January 2016
-
- Article
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
An algorithm for the principal ideal problem in indefinite quaternion algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 366-384
-
- Article
-
- You have access
- Export citation
Approximating the densest sublattice from Rankin’s inequality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 92-111
-
- Article
-
- You have access
- Export citation
Traps to the BGJT-algorithm for discrete logarithms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 218-229
-
- Article
-
- You have access
- Export citation
The discrete logarithm problem for exponents of bounded height
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 148-156
-
- Article
-
- You have access
- Export citation
Finding roots in
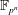 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 203-217
-
- Article
-
- You have access
- Export citation
On the computation of the determinant of vector-valued Siegel modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 247-256
-
- Article
-
- You have access
- Export citation
On the units generated by Weierstrass forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 303-313
-
- Article
-
- You have access
- Export citation
Class number calculation using Siegel functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 295-302
-
- Article
-
- You have access
- Export citation