Refine listing
Actions for selected content:
2818 results in 11xxx
ORIGAMI RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 02 November 2012, pp. 299-311
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Orderings and signatures of higher level on multirings and hyperfields
- Part of
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 May 2012, pp. 489-518
- Print publication:
- December 2012
-
- Article
- Export citation
On Greenberg’s L-invariant of the symmetric sixth power of an ordinary cusp form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1033-1050
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
CM cycles on Shimura curves, and p-adic L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1003-1032
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Structures de Hodge–Pink pour les φ/𝔖-modules de Breuil et Kisin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 03 May 2012, pp. 751-789
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Slopes of the U7 operator acting on a space of overconvergent modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 113-139
-
- Article
-
- You have access
- Export citation
On the equations a2−2b6=cp and a2−2=cp
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 158-171
-
- Article
-
- You have access
- Export citation
A crossed-product approach to the Cuntz–Li algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 429-459
-
- Article
-
- You have access
- Export citation
Averages of shifted convolutions of d3(n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 551-576
-
- Article
-
- You have access
- Export citation
ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 236-274
- Print publication:
- July 2012
-
- Article
- Export citation
THE LEAST COMMON MULTIPLE OF CONSECUTIVE TERMS IN A QUADRATIC PROGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 389-404
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On the automorphy of l-adic Galois representations with small residual image With an appendix by Robert Guralnick, Florian Herzig, Richard Taylor and Jack Thorne
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 05 April 2012, pp. 855-920
- Print publication:
- October 2012
-
- Article
- Export citation
The algebraic numbers definable in various exponential fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 April 2012, pp. 825-834
- Print publication:
- October 2012
-
- Article
- Export citation
ROOTS OF UNITY AS QUOTIENTS OF TWO ROOTS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 10 August 2012, pp. 137-144
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
COUNTING FIXED POINTS, TWO-CYCLES, AND COLLISIONS OF THE DISCRETE EXPONENTIAL FUNCTION USING p-ADIC METHODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 163-178
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
On modular inverses of cyclotomic polynomials and the magnitude oftheir coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 44-58
-
- Article
-
- You have access
- Export citation
PRODUCTS OF SHIFTED PRIMES SIMULTANEOUSLY TAKING PERFECT POWER VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 145-154
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
CAUCHY–MIRIMANOFF AND RELATED POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 269-280
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Products of three pairwise coprime integers in short intervals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 59-70
-
- Article
-
- You have access
- Export citation
SOME EXACT ALGEBRAIC EXPRESSIONS FOR THE TAILS OF TASOEV CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 179-193
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
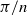


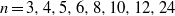

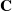


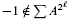 to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.
to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.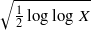 as
as 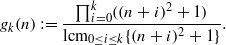
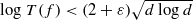 . In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field
. In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field 