Refine listing
Actions for selected content:
2818 results in 11xxx
A ONE LINE FACTORING ALGORITHM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 61-69
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
LOG-SINE EVALUATIONS OF MAHLER MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 15-36
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
VARIATIONS AROUND A PROBLEM OF MAHLER AND MENDÈS FRANCE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 37-44
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ALGEBRAIC DIVISIBILITY SEQUENCES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 24 April 2012, pp. 99-126
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
A SIMPLIFIED PROOF OF HESSELHOLT’S CONJECTURE ON GALOIS COHOMOLOGY OF WITT VECTORS OF ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 456-460
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
ON THE CLASS NUMBER AND THE FUNDAMENTAL UNIT OF THE REAL QUADRATIC FIELD

- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 359-370
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Opérateur de Lefschetz sur les tours de Drinfeld et Lubin–Tate
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 507-530
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A non-solvable extension of ℚ unramified outside 7
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 24 January 2012, pp. 669-674
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
From L-series of elliptic curves to Mahler measures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 23 January 2012, pp. 385-414
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
MOYENNES DE FONCTIONS ARITHMÉTIQUES DE FORMES BINAIRES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 19 January 2012, pp. 290-304
- Print publication:
- July 2012
-
- Article
- Export citation
Generalized affine Springer fibres
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 569-609
- Print publication:
- July 2012
-
- Article
- Export citation
Locally analytic vectors of some crystabelian representations of GL2(ℚp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 December 2011, pp. 28-64
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
QUASIMODULAR FORMS AND COHOMOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 15 December 2011, pp. 150-163
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
Geometric Weil representation in characteristic two
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 221-271
- Print publication:
- April 2012
-
- Article
- Export citation
Higher-level canonical subgroups for p-divisible groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 December 2011, pp. 363-419
- Print publication:
- April 2012
-
- Article
- Export citation
SOME REMARKS ON THE RIEMANN ZETA FUNCTION AND PRIME FACTORS OF NUMERATORS OF BERNOULLI NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 216-223
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Symmetry and parity in Frobenius action on cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 295-303
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
ON A CERTAIN CONVOLUTION OF POLYLOGARITHMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 461-472
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Proof of the Hamiltonicity-Trace Conjecture for Singularly Perturbed Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-910
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
On ramification filtrations and p-adic differential equations, II: mixed characteristic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 415-463
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation

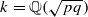 , let
, let 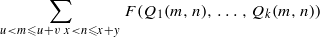
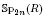 . We also construct a geometric analogue of the Weil representation of Ĝ, this is a triangulated category on which Ĝ acts by functors. This triangulated category and the action are geometric in a suitable sense.
. We also construct a geometric analogue of the Weil representation of Ĝ, this is a triangulated category on which Ĝ acts by functors. This triangulated category and the action are geometric in a suitable sense.