Refine listing
Actions for selected content:
2818 results in 11xxx
ALTERNATING EULER SUMS AND SPECIAL VALUES OF THE WITTEN MULTIPLE ZETA FUNCTION ATTACHED TO

- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 February 2011, pp. 419-430
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON FOURIER COEFFICIENTS OF MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 26 November 2010, pp. 50-62
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
ON SUMS OF FIBONACCI NUMBERS MODULO p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 413-419
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
DISTANCE BETWEEN ARITHMETIC PROGRESSIONS AND PERFECT SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 41-49
- Print publication:
- January 2011
-
- Article
- Export citation
On the gaps between values of binary quadratic forms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 01 November 2010, pp. 25-32
-
- Article
-
- You have access
- Export citation
The yoga of the Cassels–Tate pairing
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 November 2010, pp. 451-460
-
- Article
-
- You have access
- Export citation
Repunit Lehmer numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 55-65
-
- Article
-
- You have access
- Export citation
On the discrete logarithm problem in elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 October 2010, pp. 75-104
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON SPECIAL VALUES OF CERTAIN DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 435-438
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
ON COMMON DIVISORS OF MULTINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 138-157
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
ON THE BINARY DIGITS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 233-244
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
NONVANISHING OF JACOBI POINCARÉ SERIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 12 January 2011, pp. 165-179
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
CONVEX STANDARD FUNDAMENTAL DOMAIN FOR SUBGROUPS OF HECKE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 96-107
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
One level density of low-lying zeros of families of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Subconvexity for a double Dirichlet series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 355-374
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Transfert d’intégrales orbitales pour le groupe métaplectique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 524-590
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Points of low height on elliptic surfaces with torsion
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 27 August 2010, pp. 370-387
-
- Article
-
- You have access
- Export citation
Refined class number formulas and Kolyvagin systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 56-74
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Points de torsion sur les variétés abéliennes de type GSp
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 05 August 2010, pp. 27-65
- Print publication:
- January 2012
-
- Article
- Export citation
On factorials expressible as sums of at most three Fibonacci numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 747-763
-
- Article
-
- You have access
- Export citation

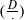 . As a consequence, using the identities of Cohen [‘Sums involving the values at negative integers of
. As a consequence, using the identities of Cohen [‘Sums involving the values at negative integers of 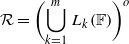
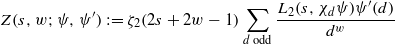
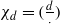 and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to
and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 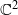 possessing a group of functional equations isomorphic to
possessing a group of functional equations isomorphic to 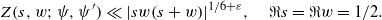
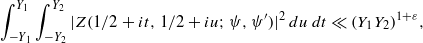
 for a non-torsion point
for a non-torsion point 