Refine listing
Actions for selected content:
2818 results in 11xxx
A p-adic analogue of the Borel regulator and the Bloch–Kato exponential map
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 149-190
- Print publication:
- January 2011
-
- Article
- Export citation
On endoscopy and the refined Gross–Prasad conjecture for (SO5, SO4)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 235-324
- Print publication:
- April 2011
-
- Article
- Export citation
Local Fourier transform and epsilon factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 1507-1551
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
Geometric level raising for p-adic automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 335-354
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
The complexity of the four colour theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 414-425
-
- Article
-
- You have access
- Export citation
THE ACTION OF HECKE OPERATORS ON HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2010, pp. 51-74
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
The Mordell–Weil sieve: proving non-existence of rational points on curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 272-306
-
- Article
-
- You have access
- Export citation
A DETERMINANT FORMULA FOR RELATIVE CONGRUENCE ZETA FUNCTIONS FOR CYCLOTOMIC FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 15 July 2010, pp. 133-144
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 July 2010, pp. 188-234
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Affine Deligne–Lusztig varieties in affine flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 1339-1382
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Fundamental domains for genus-zero and genus-one congruence subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 222-245
-
- Article
-
- You have access
- Export citation
A non-abelian Stickelberger theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 01 July 2010, pp. 35-55
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
DAVENPORT’S METHOD AND SLIM EXCEPTIONAL SETS: THE ASYMPTOTIC FORMULAE IN WARING’S PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 13 July 2010, pp. 305-321
- Print publication:
- July 2010
-
- Article
- Export citation
ALGEBRAIC VALUES OF TRANSCENDENTAL FUNCTIONS AT ALGEBRAIC POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 322-327
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF LATIN RECTANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 167-170
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
ON THE DIOPHANTINE EQUATION z2=f(x)2±f(y)2, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 187-204
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
The distribution of close conjugate algebraic numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 1165-1179
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
ON A CLASS OF GENERALIZED FERMAT EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 505-510
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON A RESULT OF RUZSA, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 340-347
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
K1 of products of Drinfeld modular curves and special values of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 886-918
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
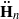 of type GL
of type GL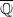 can be the exceptional set of some transcendental entire function. Furthermore, we give a much more general version of this theorem and present a unified proof.
can be the exceptional set of some transcendental entire function. Furthermore, we give a much more general version of this theorem and present a unified proof.