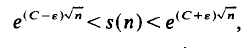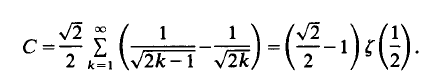Refine listing
Actions for selected content:
2838 results in 11xxx
Sums and differences of quartic norms
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-245
- Print publication:
- December 1993
-
- Article
- Export citation
On Mahler's compound bodies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-215
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
Irregularities of point distribution relative to convex polygons II
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-136
- Print publication:
- June 1993
-
- Article
- Export citation
A bound, and a conjecture, on the maximum lattice-packing density of a superball
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-143
- Print publication:
- June 1993
-
- Article
- Export citation
Long mollifiers of the Riemann Zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-87
- Print publication:
- June 1993
-
- Article
- Export citation
On the distribution of gaps between squarefree numbers
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-101
- Print publication:
- June 1993
-
- Article
- Export citation
Multiple Franel integrals
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-70
- Print publication:
- June 1993
-
- Article
- Export citation
Irregularities of point distribution relative to half-planes I
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-126
- Print publication:
- June 1993
-
- Article
- Export citation
Geometric and arithmetic postulation of the exponential function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-127
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
A problem of Good on Hausdorff dimension
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 244-246
- Print publication:
- December 1992
-
- Article
- Export citation
The spatial distribution of algebraic integers on constant-norm hypersurfaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 350-366
- Print publication:
- December 1992
-
- Article
- Export citation
On the exceptional set for the sum of a prime and a k-th power
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 400-421
- Print publication:
- December 1992
-
- Article
- Export citation
Linear equations in primes
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-378
- Print publication:
- December 1992
-
- Article
- Export citation
On Vinogradov's mean value theorem
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 379-399
- Print publication:
- December 1992
-
- Article
- Export citation
Characterization of two-distance sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 198-218
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Uniform distribution and lattice point counting
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Metrical properties of best approximants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-91
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
On Bombieri and Davenport's theorem concerning small gaps between primes
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-17
- Print publication:
- June 1992
-
- Article
- Export citation
An asymptotic formula for a-th powers dividing binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
- Print publication:
- June 1992
-
- Article
- Export citation
Simultaneous additive congruences to a large prime modulus
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1992
-
- Article
- Export citation




 is a distribution of
is a distribution of 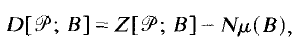
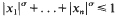 is 2
is 2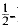 -line, where
-line, where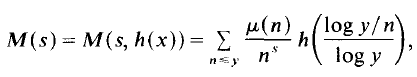
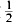 yields κ > 0·3562, having 0 < θ <
yields κ > 0·3562, having 0 < θ < 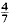 gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ <
gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ < 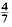 , this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.
, this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.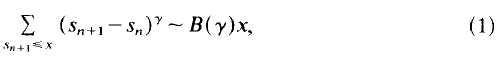
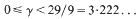
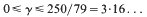

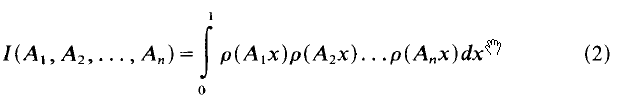
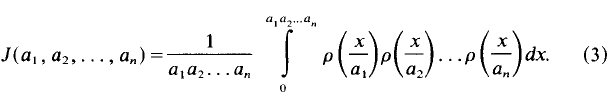
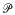 is a distribution of
is a distribution of 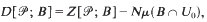
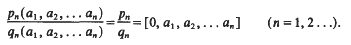
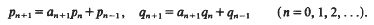
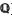 ] =
] = 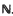 . Most of what we shall discuss is trivial when
. Most of what we shall discuss is trivial when 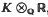 , and is to be regarded as a topological
, and is to be regarded as a topological 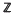 -algebra, dim
-algebra, dim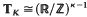 -submodule of rank
-submodule of rank 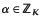 which have a fixed norm
which have a fixed norm 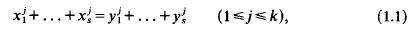
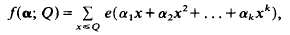
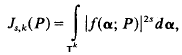
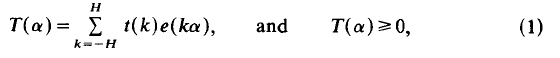
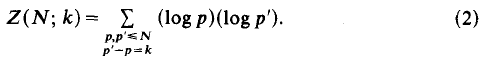
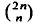 satisfies for arbitrary
satisfies for arbitrary