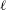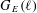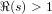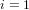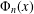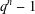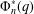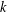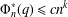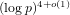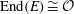Refine listing
Actions for selected content:
125 results in 11Yxx
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
Zeroes of partial sums of the zeta-function
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
A new approach to the discrete logarithm problem with auxiliary inputs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
PRIMITIVE PRIME DIVISORS AND THE
 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2015, pp. 122-135
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Two compact incremental prime sieves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 675-683
-
- Article
-
- You have access
- Export citation
EFFICIENT ALGORITHMS FOR TRAVELLING SALESMAN PROBLEMS ARISING IN WAREHOUSE ORDER PICKING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 22 September 2015, pp. 166-174
-
- Article
-
- You have access
- Export citation
A quasi-linear time algorithm for computing modular polynomials in dimension 2
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 603-632
-
- Article
-
- You have access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
BETTER BOUNDS IN CHEN’S INEQUALITIES FOR THE EULER CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 94-97
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 308-322
-
- Article
-
- You have access
- Export citation
Computing overconvergent forms for small primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 250-257
-
- Article
-
- You have access
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
An algorithm for the principal ideal problem in indefinite quaternion algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 366-384
-
- Article
-
- You have access
- Export citation
Approximating the densest sublattice from Rankin’s inequality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 92-111
-
- Article
-
- You have access
- Export citation
Traps to the BGJT-algorithm for discrete logarithms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 218-229
-
- Article
-
- You have access
- Export citation
On the units generated by Weierstrass forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 303-313
-
- Article
-
- You have access
- Export citation