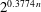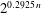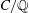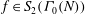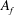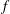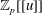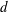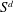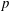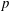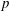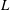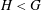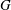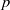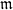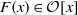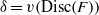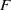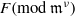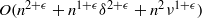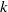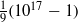Refine listing
Actions for selected content:
125 results in 11Yxx
A sieve algorithm based on overlattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 49-70
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Computing Galois representations of modular abelian surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 36-48
-
- Article
-
- You have access
- Export citation
Linear algebra over
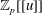 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation
Computing in quotients of rings of integers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 349-365
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
RAMANUJAN SERIES UPSIDE-DOWN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 07 July 2014, pp. 78-106
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A census of quadratic post-critically finite rational functions defined over
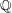 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation
Evaluating
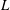 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 245-258
-
- Article
-
- You have access
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
Computation of Galois groups of rational polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
Singular values of multiple eta-quotients for ramified primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 07 November 2013, pp. 407-418
-
- Article
-
- You have access
- Export citation
Computing Borcherds products
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 200-215
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
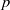 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
Václav Šimerka: quadratic forms and factorization
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 118-129
-
- Article
-
- You have access
- Export citation
Minimal solvable nonic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 130-138
-
- Article
-
- You have access
- Export citation
A GENERATING FUNCTION OF THE SQUARES OF LEGENDRE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 March 2013, pp. 125-131
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
A linear recurrence sequence of composite numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 November 2012, pp. 360-373
-
- Article
-
- You have access
- Export citation