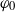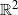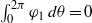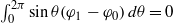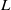Refine listing
Actions for selected content:
134 results in 35Cxx
A sharp ultimate bound of the solutions to some second-order evolution equations with nonlinear damping
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 22 July 2015, pp. 703-714
- Print publication:
- August 2015
-
- Article
- Export citation
A DIFFUSIVE LOGISTIC EQUATION WITH MEMORY IN BESSEL POTENTIAL SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 251-258
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
CANARDS IN ADVECTION–REACTION–DIFFUSION SYSTEMS IN ONE SPATIAL DIMENSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 342-343
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
ON A CLASS OF ELLIPTIC SYSTEM OF SCHRÖDINGER–POISSON TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 301-314
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Multitype Branching Brownian Motion and Traveling Waves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 217-240
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
An Application of the Backbone Decomposition to Supercritical Super-Brownian Motion with a Barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 671-684
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
ELLIPTIC EXTENSIONS IN THE DISK WITH OPERATORS IN DIVERGENCE FORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 20 August 2012, pp. 51-55
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
REGULARITY OF SOLUTIONS TO A TIME-FRACTIONAL DIFFUSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 July 2011, pp. 123-138
-
- Article
-
- You have access
- Export citation
Time-isolated Singularities of Temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-429
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Initial and relative limiting behaviour of temperatures on a strip
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-228
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
Representation theorems for parabolic systems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-288
- Print publication:
- April 1982
-
- Article
-
- You have access
- Export citation
On a method for constructing Bergman kernels
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 454-461
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
Integral representations of solutions to a class of fourth order elliptic equations in three independent variables
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 283-290
- Print publication:
- December 1971
-
- Article
- Export citation
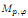 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global