Refine listing
Actions for selected content:
134 results in 35Cxx
INTEGRAL EQUATION FORMULATION FOR SHOUT OPTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 08 August 2018, pp. 65-85
-
- Article
-
- You have access
- Export citation
Solving the Equation
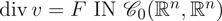 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1055-1061
-
- Article
- Export citation
ON DEGENERATE SIGMA-FUNCTIONS IN GENUS 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 25 June 2018, pp. 169-193
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
ON SYSTEMS OF PARTIAL DIFFERENTIAL EQUATIONS OF BRIOT–BOUQUET TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 122-133
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Classification of extinction profiles for a one-dimensional diffusive Hamilton–Jacobi equation with critical absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 559-574
- Print publication:
- June 2018
-
- Article
- Export citation
Poincaré inequalities for Sobolev spaces with matrix-valued weights and applications to degenerate partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 April 2018, pp. 61-100
- Print publication:
- February 2019
-
- Article
- Export citation
EXISTENCE OF TRAVELLING WAVES IN THE FRACTIONAL BURGERS EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 102-109
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Infinitely many solutions for equations of p(x)-Laplace type with the nonlinear Neumann boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 August 2017, pp. 1-31
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
A Moving Mesh Finite Difference Method for Non-Monotone Solutions of Non-Equilibrium Equations in Porous Media
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 935-964
- Print publication:
- October 2017
-
- Article
- Export citation
Initial–boundary-value problems for one-dimensional compressible Navier–Stokes equations with degenerate transport coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 935-969
- Print publication:
- October 2017
-
- Article
- Export citation
Existence of travelling pulses in a neural model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 397-427
- Print publication:
- April 2017
-
- Article
- Export citation
Stability and Unstability of the Standing Wave to Euler Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 818-838
- Print publication:
- August 2017
-
- Article
- Export citation
Neumann to Steklov eigenvalues: asymptotic and monotonicity results
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 429-447
- Print publication:
- April 2017
-
- Article
- Export citation
New Non-Travelling Wave Solutions of Calogero Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1036-1049
- Print publication:
- December 2016
-
- Article
- Export citation
Existence and linearized stability of solitary waves for a quasilinear Benney system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 21 March 2016, pp. 547-564
- Print publication:
- June 2016
-
- Article
- Export citation
A convergence result for the ergodic problem for Hamilton–Jacobi equations with Neumann-type boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 225-242
- Print publication:
- April 2016
-
- Article
- Export citation
Fast-moving finite and infinite trains of solitons for nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1251-1282
- Print publication:
- December 2015
-
- Article
- Export citation
GROUP FOLIATION OF DIFFERENTIAL EQUATIONS USING MOVING FRAMES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 26 October 2015, e22
-
- Article
-
- You have access
- Open access
- Export citation
Instability of periodic traveling waves for the symmetric regularized long wave equation
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 235-268
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Cylindrically symmetric travelling fronts in a periodic reaction—diffusion equation with bistable nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 28 August 2015, pp. 1053-1090
- Print publication:
- October 2015
-
- Article
- Export citation
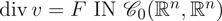

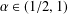
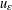
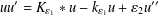
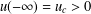
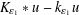
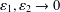
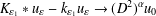
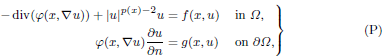
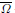
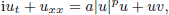
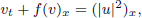
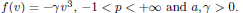 , –1 <
, –1 < 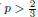 . We also show the existence of standing waves in the case
. We also show the existence of standing waves in the case 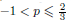 , with compact support if – 1 <
, with compact support if – 1 < 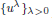 to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini
to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini 