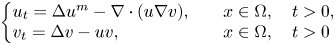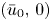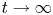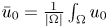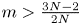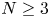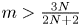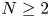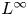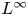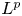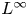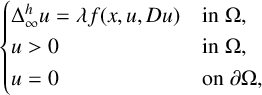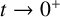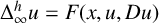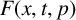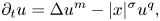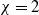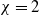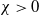Refine listing
Actions for selected content:
134 results in 35Cxx
Travelling wave solutions and spreading speeds for a scalar age-structured equation with nonlocal diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 856-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 1. The Cauchy problem on the real line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 October 2024, pp. 775-810
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling wavefronts for the Belousov–Zhabotinsky system with non-local delayed interaction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 738-774
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling waves with continuous profile for hyperbolic Keller-Segel equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 584-612
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-linear biphasic mixture model: Existence and uniqueness results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 161-185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 178-209
- Print publication:
- April 2025
-
- Article
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
Diffuse-interface approximation and weak–strong uniqueness of anisotropic mean curvature flow
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 82-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1377-1397
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 345-374
- Print publication:
- December 2024
-
- Article
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-22
-
- Article
- Export citation
Derivation and travelling wave analysis of phenotype-structured haptotaxis models of cancer invasion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 February 2024, pp. 231-263
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adhesion and volume filling in one-dimensional population dynamics under Dirichlet boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1174-1222
- Print publication:
- August 2025
-
- Article
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 December 2023, pp. 118-148
- Print publication:
- February 2025
-
- Article
- Export citation
Analysis and numerical simulations of travelling waves due to plant–soil negative feedback
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 07 December 2023, pp. 554-565
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of renormalized solutions to fully anisotropic and inhomogeneous elliptic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 31 October 2023, pp. 821-857
- Print publication:
- June 2025
-
- Article
- Export citation
Generic ill-posedness of the energy–momentum equations and differential inclusions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 26 September 2023, pp. 470-495
- Print publication:
- April 2025
-
- Article
- Export citation
Generalised solution to a 2D parabolic-parabolic chemotaxis system for urban crime: Global existence and large-time behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 409-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation