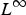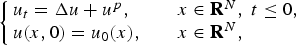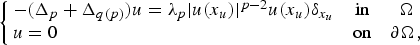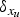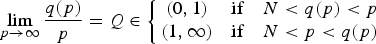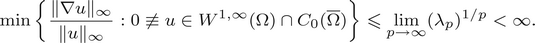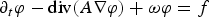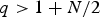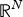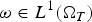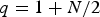Refine listing
Actions for selected content:
134 results in 35Cxx
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
Existence, uniqueness and stability of transition fronts of non-local equations in time heterogeneous bistable media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 28 August 2019, pp. 601-645
-
- Article
- Export citation
Existence of multi-travelling waves in capillary fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2905-2936
- Print publication:
- December 2020
-
- Article
- Export citation
Distributions as initial values in a triangular hyperbolic system of conservation laws
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 July 2019, pp. 2757-2775
- Print publication:
- December 2020
-
- Article
- Export citation
Analysis of spreading speeds for monotone semiflows with an application to CNNs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 06 March 2019, pp. 369-384
-
- Article
- Export citation
A pointwise characterisation of the PDE system of vectorial calculus of variations in L∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1653-1669
- Print publication:
- August 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
A stability index for travelling waves in activator-inhibitor systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 517-548
- Print publication:
- February 2020
-
- Article
- Export citation
An application of the theorem on Sums to viscosity solutions of degenerate fully nonlinear equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 975-992
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotically self-similar behaviour of global solutions for semilinear heat equations with algebraically decaying initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 789-811
- Print publication:
- April 2020
-
- Article
- Export citation
Long-time asymptotic expansions for Navier-Stokes equations with power-decaying forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 569-606
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
- Print publication:
- December 2019
-
- Article
- Export citation
Logarithmic upper bounds for weak solutions to a class of parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1481-1491
- Print publication:
- December 2019
-
- Article
- Export citation
Asymptotic approximations for the plasmon resonances of nearly touching spheres
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 246-276
-
- Article
- Export citation
Existence of travelling waves with the critical speed for an influenza model with treatment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 232-245
-
- Article
- Export citation
Continuous solutions and approximating scheme for fractional Dirichlet problems on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 533-560
- Print publication:
- April 2019
-
- Article
- Export citation
Multiscale modelling and homogenisation of fibre-reinforced hydrogels for tissue engineering
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 22 November 2018, pp. 143-171
-
- Article
-
- You have access
- Export citation
SPATIAL HAMILTONIAN IDENTITIES FOR NONLOCALLY COUPLED SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 14 November 2018, e22
-
- Article
-
- You have access
- Open access
- Export citation
On the avascular ellipsoidal tumour growth model within a nutritive environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 111-142
-
- Article
- Export citation
The time-dependent Schrödinger equation with piecewise constant potentials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 57-83
-
- Article
- Export citation