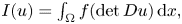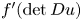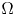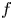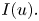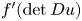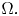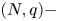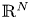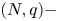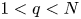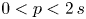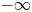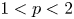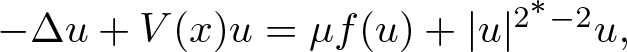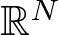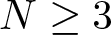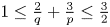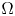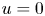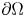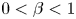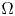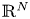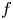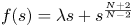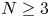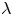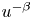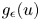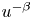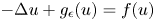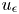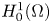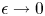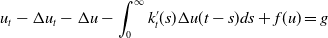Refine listing
Actions for selected content:
134 results in 35Cxx
On a class of special Euler–Lagrange equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 21 September 2023, pp. 429-452
- Print publication:
- April 2025
-
- Article
- Export citation
Periodic and solitary waves in a Korteweg–de Vries equation with delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 176-198
- Print publication:
- February 2025
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
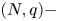 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$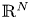 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 124-175
- Print publication:
- February 2025
-
- Article
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1313-1335
- Print publication:
- October 2024
-
- Article
- Export citation
A non-periodic indefinite variational problem in ℝN with critical exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 579-612
-
- Article
- Export citation
Interface behaviour of the slow diffusion equation with strong absorption: Intermediate-asymptotic properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1099-1132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of minima for nonlocal operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 23 May 2023, pp. 1033-1046
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extended symmetry analysis of remarkable (1+2)-dimensional Fokker–Planck equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1067-1098
-
- Article
- Export citation
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 727-745
- Print publication:
- June 2024
-
- Article
- Export citation
Exact nonclassical symmetry solutions of Lotka–Volterra-type population systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 998-1016
-
- Article
- Export citation
Branching Brownian motion in a periodic environment and uniqueness of pulsating traveling waves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 510-548
- Print publication:
- June 2023
-
- Article
- Export citation
Modelling, simulation and optimisation of parabolic trough power plants
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 592-615
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Long-time asymptotics of the modified KdV equation in weighted Sobolev spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 August 2022, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Harnack inequality for the nonlocal equations with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1479-1502
- Print publication:
- October 2023
-
- Article
- Export citation
Convergence to a self-similar solution for a one-phase Stefan problem arising in corrosion theory
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 701-737
-
- Article
- Export citation
Singular elliptic equations with nonlinearities of subcritical and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 27 July 2022, pp. 652-690
-
- Article
- Export citation
The nonclassical diffusion equations with time-dependent memory kernels and a new class of nonlinearities
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 February 2022, pp. 716-733
- Print publication:
- September 2022
-
- Article
- Export citation
Existence and uniqueness of solutions to a flow and transport problem with degenerating coefficients
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 55-76
-
- Article
-
- You have access
- HTML
- Export citation
Exact solutions and critical behaviour for a linear growth-diffusion equation on a time-dependent domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 53-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear PDE with constant coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. S2-S27
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation