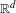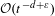Refine listing
Actions for selected content:
112 results in 35Lxx
1D Exact Elastic-Perfectly Plastic Solid Riemann Solver and Its Multi-Material Application
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 621-650
- Print publication:
- June 2017
-
- Article
- Export citation
Convergence of Monotone Schemes for Conservation Laws with Zero-Flux Boundary Conditions
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 515-542
- Print publication:
- June 2017
-
- Article
- Export citation
A Mathematical Analysis of Scale Similarity
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 149-161
- Print publication:
- January 2017
-
- Article
- Export citation
Numerical Study of Nanosecond Pulsed Plasma Actuator in Laminar Flat Plate Boundary Layer
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1424-1442
- Print publication:
- November 2016
-
- Article
- Export citation
Runge-Kutta Discontinuous Galerkin Method with Front Tracking Method for Solving the Compressible Two-Medium Flow on Unstructured Meshes
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 73-91
- Print publication:
- February 2017
-
- Article
- Export citation
Two-Size Moment Multi-Fluid Model: A Robust and High-Fidelity Description of Polydisperse Moderately Dense Evaporating Sprays
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 902-943
- Print publication:
- October 2016
-
- Article
- Export citation
Godunov-Type Numerical Methods for a Model of Granular Flow on Open Tables with Walls
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1071-1105
- Print publication:
- October 2016
-
- Article
- Export citation
Practical Techniques in Ghost Fluid Method for Compressible Multi-Medium Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 619-659
- Print publication:
- September 2016
-
- Article
- Export citation
Extended Hydrodynamic Models and Multigrid Solver of a Silicon Diode Simulation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 551-582
- Print publication:
- September 2016
-
- Article
- Export citation
Well-posedness and regularity of linear hyperbolic systems with dynamic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1047-1080
- Print publication:
- October 2016
-
- Article
- Export citation
Directly Simulation of Second Order Hyperbolic Systems in Second Order Form via the Regularization Concept
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 86-135
- Print publication:
- July 2016
-
- Article
- Export citation
An All-Regime Lagrange-Projection Like Scheme for the Gas Dynamics Equations on Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 188-233
- Print publication:
- July 2016
-
- Article
- Export citation
High-Order Mesh Generation for Discontinuous Galerkin Methods Based on Elastic Deformation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 693-702
- Print publication:
- August 2016
-
- Article
- Export citation
Periodic Navier Solutions for the Plate Equation with Non-Monotone Nonlinearities: the Multidimensional Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 203-230
-
- Article
- Export citation
Entropy Stable Scheme on Two-Dimensional Unstructured Grids for Euler Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1111-1140
- Print publication:
- May 2016
-
- Article
- Export citation
Analyses and Applications of the Second-Order Cross Correlation in the Passive Imaging
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1191-1220
- Print publication:
- May 2016
-
- Article
- Export citation
Runge-Kutta Discontinuous Galerkin Method with a Simple and Compact Hermite WENO Limiter
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 944-969
- Print publication:
- April 2016
-
- Article
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
- Print publication:
- June 2018
-
- Article
- Export citation
A SOLUTION OF THE CONSERVATION LAW FORM OF THE SERRE EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 28 March 2016, pp. 385-394
-
- Article
-
- You have access
- Open access
- Export citation
Development of a Combined Compact Difference Scheme to Simulate Soliton Collision in a Shallow Water Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 603-631
- Print publication:
- March 2016
-
- Article
- Export citation
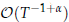 , with 0 <
, with 0 <