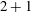Refine listing
Actions for selected content:
112 results in 35Lxx
Traffic Lights or Roundabout? Analysis using the Modified Kinematic LWR Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 80-88
- Print publication:
- February 2016
-
- Article
- Export citation
Mathematical Models for the Propagation of Stress Waves in Elastic Rods: Exact Solutions and Numerical Simulation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 257-270
- Print publication:
- April 2016
-
- Article
- Export citation
Geometric Numerical Integration for Peakon b-Family Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 15 January 2016, pp. 24-52
- Print publication:
- January 2016
-
- Article
- Export citation
Relaxation Schemes for the M1 Model with Space-Dependent Flux: Application to Radiotherapy Dose Calculation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 15 January 2016, pp. 168-191
- Print publication:
- January 2016
-
- Article
- Export citation
A Front Tracking Method for the Simulation of Compressible Multimedium Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 15 January 2016, pp. 124-142
- Print publication:
- January 2016
-
- Article
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
- Print publication:
- 2016
-
- Article
- Export citation
Dynamics in the fundamental solution of a non-convex conservation law
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 169-193
- Print publication:
- February 2016
-
- Article
- Export citation
Lp -type pullback attractors for a semilinear heat equation on time-varying domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1029-1052
- Print publication:
- October 2015
-
- Article
- Export citation
Convergence Study of Moment Approximations for Boundary Value Problems of the Boltzmann-BGK Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 14 September 2015, pp. 529-557
- Print publication:
- September 2015
-
- Article
- Export citation
Effect of Geometric Conservation Law on Improving Spatial Accuracy for Finite Difference Schemes on Two-Dimensional Nonsmooth Grids
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 14 September 2015, pp. 673-706
- Print publication:
- September 2015
-
- Article
- Export citation
Boundary effects and large-time behaviour for quasilinear equations with nonlinear damping
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 26 August 2015, pp. 959-978
- Print publication:
- October 2015
-
- Article
- Export citation
Long Time Behaviour of an Exponential Integrator for a Vlasov-Poisson System with Strong Magnetic Field
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 2 / August 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 263-296
- Print publication:
- August 2015
-
- Article
- Export citation
A sharp ultimate bound of the solutions to some second-order evolution equations with nonlinear damping
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 22 July 2015, pp. 703-714
- Print publication:
- August 2015
-
- Article
- Export citation
Blow-up for the wave equation with nonlinear source and boundary damping terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 20 July 2015, pp. 759-778
- Print publication:
- August 2015
-
- Article
- Export citation
GPU Accelerated Discontinuous Galerkin Methods for Shallow Water Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 37-64
- Print publication:
- July 2015
-
- Article
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
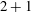 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
On the existence of global weak solutions to an integrable two-component Camassa–Holm shallow-water system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 755-775
-
- Article
-
- You have access
- Export citation
NONLINEAR WAVE EQUATIONS AND REACTION–DIFFUSION EQUATIONS WITH SEVERAL NONLINEAR SOURCE TERMS OF DIFFERENT SIGNS AT HIGH ENERGY LEVEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 153-170
-
- Article
-
- You have access
- Export citation
Singular solutions of a fully nonlinear 2 × 2 system of conservation laws
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 30 August 2012, pp. 711-729
-
- Article
-
- You have access
- Export citation
Improved local energy decay for the wave equation on asymptotically Euclidean odd dimensional manifolds in the short range case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 July 2012, pp. 635-650
- Print publication:
- July 2013
-
- Article
- Export citation