In this paper, some existence and uniqueness results for generalized solutions to a periodic-Dirichlet problem for semilinear wave equations are given, using a global inverse function theorem. These results extend those known in the literature.

We use the compensated compactness method coupled with some basic ideas of kinetic formulation developed by Lions, Perthame, Souganidis and Tadmor to give a refined proof for the existence of global bounded entropy solutions to the Le Roux system. This new method of the reduction of Young measures can be applied to solve other problems.

Theorems on the Fredholm alternative and well-posedness of the characteristic initial-value problem

are established, where l : C(;ℝ) is a linear bounded operator, q ∈ L(;ℝ), ϕ:[a,b]→ℝ, ψ:[c,d]→ℝ are absolutely continuous functions and =[a,b]×[c,d]. Some solvability conditions of the problem considered are also given.

We extend Penrose's peeling model for the asymptotic behaviour of solutions to the scalar wave equation at null infinity on asymptotically flat backgrounds, which is well understood for flat space-time, to Schwarzschild and the asymptotically simple space-times of Corvino–Schoen/Chrusciel–Delay. We combine conformal techniques and vector field methods: a naive adaptation of the ‘Morawetz vector field’ to a conformal rescaling of the Schwarzschild metric yields a complete scattering theory on Corvino–Schoen/Chrusciel–Delay space-times. A good classification of solutions that peel arises from the use of a null vector field that is transverse to null infinity to raise the regularity in the estimates. We obtain a new characterization of solutions admitting a peeling at a given order that is valid for both Schwarzschild and Minkowski space-times. On flat space-time, this allows larger classes of solutions than the characterizations used since Penrose's work. Our results establish the validity of the peeling model at all orders for the scalar wave equation on the Schwarzschild metric and on the corresponding Corvino–Schoen/Chrusciel–Delay space-times.

In this paper we study different types of planar random motions (performed with constant velocity) with three directions, defined by the vectors dj = (cos(2πj/3), sin(2πj/3)) for j = 0, 1, 2, changing at Poisson-paced times. 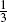We examine the cyclic motion (where the change of direction is deterministic), the completely uniform motion (where at each Poisson event each direction can be taken with probability ) and the symmetrically deviating case (where the particle can choose all directions except that taken before the Poisson event). For each of the above random motions we derive the explicit distribution of the position of the particle, by using an approach based on order statistics. We prove that the densities obtained are solutions of the partial differential equations governing the processes. We are also able to give the explicit distributions on the boundary and, for the case of the symmetrically deviating motion, we can write it as the distribution of a telegraph process. 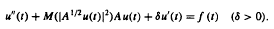For the symmetrically deviating motion we use a generalization of the Bose-Einstein statistics in order to determine the distribution of the triple (N0, N1, N2) (conditional on N(t) = k, with N0 + N1 + N2 = N(t) + 1, where N(t) is the number of Poisson events in [0, t]), where Nj denotes the number of times the direction dj (j = 0, 1, 2) is taken. Possible extensions to four directions or more are briefly considered.

In this paper we study a planar random motion (X(t), Y(t)), t>0, with orthogonal directions taken cyclically at Poisson paced times. The process is split into one-dimensional motions with alternating displacements interrupted by exponentially distributed stops. The distributions of X = X(t) (conditional and nonconditional) are obtained by means of order statistics and the connection with the telegrapher's process is derived and discussed. We are able to prove that the distributions involved in our analysis are solutions of a certain differential system and of the related fourth-order hyperbolic equation.

We will show the existence, uniqueness and regularity of global solutions for the Cauchy problem for nonlinear evolution equations with the damping term .

As an application of our results, we give the global solvability and regularity of the mixed problem with Dirichiet boundary conditions:

In this paper we consider the stochastic wave equation in one spatial dimension driven by a two-parameter Gaussian noise which is white in time and has general spatial covariance. We give conditions on the spatial covariance of the driving noise sufficient for the string to have finite expected energy and calculate this energy as a function of time. We show that these same conditions on the spatial covariance of the driving noise are also sufficient to guarantee that the energy of the string has a version which is continuous almost surely.

The aim of the present paper is to introduce some techniques, based on the change of variable formula for processes of finite variation, for establishing (integro) differential equations for evaluating the distribution of jump processes for a fixed period of time. This is of interest in insurance mathematics for evaluating the distribution of the total amount of claims occurred over some period of time, and attention will be given to such issues. Firstly we will study some techniques when the process has independent increments, and then a more refined martingale technique is discussed. The building blocks are delivered by the theory of marked point processes and associated martingale theory. A simple numerical example is given.

The present paper proposes a general approach for finding differential equations to evaluate probabilities of ruin in finite and infinite time. Attention is given to real-valued non-diffusion processes where a Markov structure is obtainable. Ruin is allowed to occur upon a jump or between the jumps. The key point is to define a process of conditional ruin probabilities and identify this process stopped at the time of ruin as a martingale. Using the theory of marked point processes together with the change-of-variable formula or the martingale representation theorem for point processes, we obtain differential equations for evaluating the probability of ruin.

Numerical illustrations are given by solving a partial differential equation numerically to obtain the probability of ruin over a finite time horizon.

Local uniqueness of solutions of the characteristic Cauchy problem is shown for operators which are perturbations of operators which already have such a uniqueness.