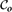Refine listing
Actions for selected content:
1446 results in 60Kxx
ADDITIVITY PROPERTIES OF SOFIC ENTROPY AND MEASURES ON MODEL SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 31 August 2016, e25
-
- Article
-
- You have access
- Open access
- Export citation
On the equivalence of systems of different sizes, with applications to system comparisons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 332-348
- Print publication:
- June 2016
-
- Article
- Export citation
Jackson networks in nonautonomous random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 315-331
- Print publication:
- June 2016
-
- Article
- Export citation
Probabilistic cellular automata with general alphabets possessing a Markov chain as an invariant distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 369-391
- Print publication:
- June 2016
-
- Article
- Export citation
Extreme paths in oriented two-dimensional percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 369-380
- Print publication:
- June 2016
-
- Article
- Export citation
Stability of multiclass queueing networks under longest-queue and longest-dominating-queue scheduling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 421-433
- Print publication:
- June 2016
-
- Article
- Export citation
Routeing on trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 475-488
- Print publication:
- June 2016
-
- Article
- Export citation
Optimal dividend and reinsurance in the presence of two reinsurers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 554-571
- Print publication:
- June 2016
-
- Article
- Export citation
Convergence of tandem Brownian queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 585-592
- Print publication:
- June 2016
-
- Article
- Export citation
On a class of multivariate counting processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 443-462
- Print publication:
- June 2016
-
- Article
- Export citation
Forward Clusters for Degenerate Random Environments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 24 May 2016, pp. 744-765
-
- Article
- Export citation
Optimal Strategy for Limit Order Book Submissions in High Frequency Trading
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 222-234
- Print publication:
- May 2016
-
- Article
- Export citation
SIR epidemics on a scale-free spatial nested modular network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 137-162
- Print publication:
- March 2016
-
- Article
- Export citation
Markov-modulated Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 235-254
- Print publication:
- March 2016
-
- Article
- Export citation
Correlation formulas for Markovian network processes in a random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 176-198
- Print publication:
- March 2016
-
- Article
- Export citation
Queues with advanced reservations: an infinite-server proxy for the bookings diary
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 13-31
- Print publication:
- March 2016
-
- Article
- Export citation
On comparing coherent systems with heterogeneous components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 88-111
- Print publication:
- March 2016
-
- Article
- Export citation
A comparison of random walks in dependent random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 199-214
- Print publication:
- March 2016
-
- Article
- Export citation
PINNING ON A DEFECT LINE: CHARACTERIZATION OF MARGINAL DISORDER RELEVANCE AND SHARP ASYMPTOTICS FOR THE CRITICAL POINT SHIFT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 29 January 2016, pp. 305-346
- Print publication:
- April 2018
-
- Article
- Export citation
Erratum to: Mixture representations of residual lifetimes of used systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1183-1186
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation