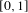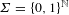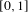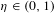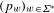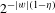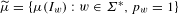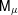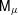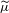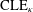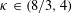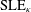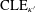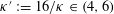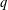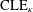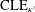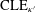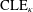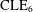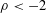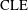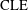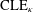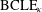Refine listing
Actions for selected content:
1446 results in 60Kxx
On an ageing class based on the moment generating function order
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 402-415
- Print publication:
- June 2018
-
- Article
- Export citation
Stochastic comparisons of coherent systems under different random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 459-472
- Print publication:
- June 2018
-
- Article
- Export citation
Spectral bounds in random graphs applied to spreading phenomena and percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 480-503
- Print publication:
- June 2018
-
- Article
- Export citation
A quenched central limit theorem for biased random walks on supercritical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 610-626
- Print publication:
- June 2018
-
- Article
- Export citation
Jante's law process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 414-439
- Print publication:
- June 2018
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
- Print publication:
- January 2020
-
- Article
- Export citation
On a jump-telegraph process driven by an alternating fractional Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 94-111
- Print publication:
- March 2018
-
- Article
- Export citation
Functional limit theorems for the number of busy servers in a G/G/∞ queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 15-29
- Print publication:
- March 2018
-
- Article
- Export citation
Univariate and multivariate stochastic comparisons and ageing properties of the generalized Pólya process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 233-253
- Print publication:
- March 2018
-
- Article
- Export citation
Percolation results for the continuum random cluster model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 231-244
- Print publication:
- March 2018
-
- Article
- Export citation
Degree-dependent threshold-based random sequential adsorption on random trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 302-326
- Print publication:
- March 2018
-
- Article
- Export citation
Asymptotic shape and the speed of propagation of continuous-time continuous-space birth processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 74-101
- Print publication:
- March 2018
-
- Article
- Export citation
The failure probability of components in three-state networks with applications to age replacement policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1051-1070
- Print publication:
- December 2017
-
- Article
- Export citation
Jigsaw percolation on random hypergraphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1261-1277
- Print publication:
- December 2017
-
- Article
- Export citation
Large-scale join-idle-queue system with general service times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 995-1007
- Print publication:
- December 2017
-
- Article
- Export citation
Traffic flow densities in large transport networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1091-1115
- Print publication:
- December 2017
-
- Article
- Export citation
On the Ornstein–Zernike equation for stationary cluster processes and the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1260-1287
- Print publication:
- December 2017
-
- Article
- Export citation
CLE PERCOLATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
Implicit renewal theory in the arithmetic case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 732-749
- Print publication:
- September 2017
-
- Article
- Export citation
Overly determined agents prevent consensus in a generalized Deffuant model on ℤ with dispersed opinions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 722-744
- Print publication:
- September 2017
-
- Article
- Export citation