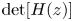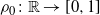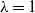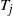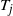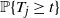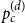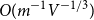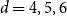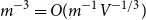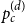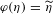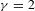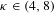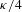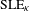Refine listing
Actions for selected content:
1446 results in 60Kxx
Percolation on an infinitely generated group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 587-615
-
- Article
- Export citation
EXPLICIT SOLUTIONS FOR CONTINUOUS-TIME QBD PROCESSES BY USING RELATIONS BETWEEN MATRIX GEOMETRIC ANALYSIS AND THE PROBABILITY GENERATING FUNCTIONS METHOD
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 03 January 2020, pp. 565-580
-
- Article
- Export citation
Runoff on rooted trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1065-1085
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Piecewise deterministic processes following two alternating patterns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1006-1019
- Print publication:
- December 2019
-
- Article
- Export citation
Exact sampling for some multi-dimensional queueing models with renewal input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1179-1208
- Print publication:
- December 2019
-
- Article
- Export citation
Cluster Expansions for GIBBS Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1129-1178
- Print publication:
- December 2019
-
- Article
- Export citation
Insensitivity of the mean field limit of loss systems under SQ(d) routeing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1027-1066
- Print publication:
- December 2019
-
- Article
- Export citation
COVER TIME FOR THE FROG MODEL ON TREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 November 2019, e41
-
- Article
-
- You have access
- Open access
- Export citation
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
ORDERING RESULTS ON EXTREMES OF EXPONENTIATED LOCATION-SCALE MODELS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 331-354
-
- Article
- Export citation
First displacement time of a tagged particle in a stochastic cluster in a simple exclusion process with random slow bonds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 717-744
- Print publication:
- September 2019
-
- Article
- Export citation
Transient and slim versus recurrent and fat: Random walks and the trees they grow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 769-786
- Print publication:
- September 2019
-
- Article
- Export citation
Comparing lifetimes of coherent systems with dependent components operating in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 937-957
- Print publication:
- September 2019
-
- Article
- Export citation
The exact asymptotics of the large deviation probabilities in the multivariate boundary crossing problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 835-864
- Print publication:
- September 2019
-
- Article
- Export citation
Boundary effect in competition processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 750-768
- Print publication:
- September 2019
-
- Article
- Export citation
Limit theorems for some skew products with mixing base maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 August 2019, pp. 241-271
- Print publication:
- January 2021
-
- Article
- Export citation
Expansion of Percolation Critical Points for Hamming Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 August 2019, pp. 68-100
-
- Article
- Export citation
Positive association of the oriented percolation cluster in randomly oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 July 2019, pp. 811-815
-
- Article
- Export citation
UNIQUENESS OF THE WELDING PROBLEM FOR SLE AND LIOUVILLE QUANTUM GRAVITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 July 2019, pp. 757-783
- Print publication:
- May 2021
-
- Article
- Export citation
ON VARIABILITY OF SERIES AND PARALLEL SYSTEMS WITH HETEROGENEOUS COMPONENTS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 626-645
-
- Article
- Export citation