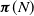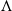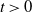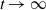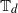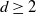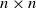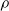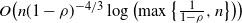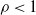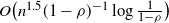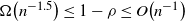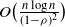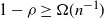Refine listing
Actions for selected content:
1446 results in 60Kxx
Exponential ergodicity and steady-state approximations for a class of markov processes under fast regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 1-29
- Print publication:
- March 2021
-
- Article
- Export citation
Branching processes with interactions: subcritical cooperative regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 251-278
- Print publication:
- March 2021
-
- Article
- Export citation
Simple peeling of planar maps with application to site percolation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 907-941
- Print publication:
- August 2022
-
- Article
- Export citation
Stochastic comparisons and ageing properties of an extended gamma process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 140-163
- Print publication:
- March 2021
-
- Article
- Export citation
AN OPTIMAL LINEAR FILTER FOR ESTIMATION OF RANDOM FUNCTIONS IN HILBERT SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 07 January 2021, pp. 274-301
-
- Article
-
- You have access
- Export citation
One-sided reflected Brownian motions and the KPZ fixed point
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 December 2020, e63
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendumto: Asymptotic shape and the speed of propagation of continuous-time continuous-space birth processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1325-1327
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Characterization of the conditional stationary distribution in Markov chains via systems of linear inequalities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1249-1283
- Print publication:
- December 2020
-
- Article
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
Geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1085-1126
- Print publication:
- December 2020
-
- Article
- Export citation
Multivariate finite-support phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1260-1275
- Print publication:
- December 2020
-
- Article
- Export citation
Synchronized Lévy queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1222-1233
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
On a new stochastic model for cascading failures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1150-1161
- Print publication:
- December 2020
-
- Article
- Export citation
On Λ-Fleming–Viot processes with general frequency-dependent selection
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1162-1197
- Print publication:
- December 2020
-
- Article
- Export citation
Non-existence of bi-infinite geodesics in the exponential corner growth model
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e46
-
- Article
-
- You have access
- Open access
- Export citation
Existence of Gibbs point processes with stable infinite range interaction
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 775-791
- Print publication:
- September 2020
-
- Article
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
- Print publication:
- September 2020
-
- Article
- Export citation
Renewal in Hawkes processes with self-excitation and inhibition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 879-915
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
On some threshold-one attractive interacting particle systems on homogeneous trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 866-898
- Print publication:
- September 2020
-
- Article
- Export citation
Improved queue-size scaling for input-queued switches via graph factorization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 798-824
- Print publication:
- September 2020
-
- Article
- Export citation