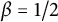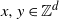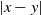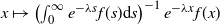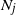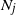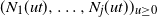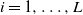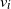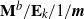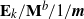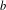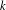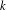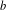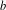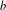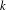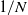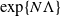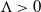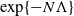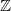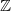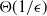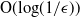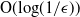Refine listing
Actions for selected content:
1446 results in 60Kxx
A note related to the CS decomposition and the BK inequality for discrete determinantal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 October 2022, pp. 189-203
- Print publication:
- March 2023
-
- Article
- Export citation
Percolation probability and critical exponents for site percolation on the UIPT
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 20 October 2022, pp. 1869-1903
- Print publication:
- December 2023
-
- Article
- Export citation
Graph distances in scale-free percolation: the logarithmic case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 295-313
- Print publication:
- March 2023
-
- Article
- Export citation
Stationary analysis of an (R, Q) inventory model with normal and emergency orders
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 106-126
- Print publication:
- March 2023
-
- Article
- Export citation
Large-scale behavior of a particle system with mean-field interaction: Traveling wave solutions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 245-274
- Print publication:
- March 2023
-
- Article
- Export citation
Interacting urns on a finite directed graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 166-188
- Print publication:
- March 2023
-
- Article
- Export citation
A Markov jump process associated with the matrix-exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 1-13
- Print publication:
- March 2023
-
- Article
- Export citation
On the study of the running maximum and minimum level of level-dependent quasi-birth–death processes and related models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 14-29
- Print publication:
- March 2023
-
- Article
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 45-67
- Print publication:
- March 2023
-
- Article
- Export citation
Optimal redundancy allocation in coherent systems with heterogeneous dependent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2022, pp. 1144-1177
- Print publication:
- December 2022
-
- Article
- Export citation
The direct-connectedness function in the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 August 2022, pp. 179-222
- Print publication:
- March 2023
-
- Article
- Export citation
Simple analytical solutions for the
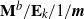 $\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$,
$\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$, 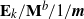 $\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$, and related queues
$\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$, and related queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1129-1143
- Print publication:
- December 2022
-
- Article
- Export citation
Construction of aggregation paradoxes through load-sharing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 223-244
- Print publication:
- March 2023
-
- Article
- Export citation
Interacting nonlinear reinforced stochastic processes: Synchronization or non-synchronization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 275-320
- Print publication:
- March 2023
-
- Article
- Export citation
Rate of convergence for particle approximation of PDEs in Wasserstein space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 28 July 2022, pp. 992-1008
- Print publication:
- December 2022
-
- Article
- Export citation
Mutually interacting superprocesses with migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 904-929
- Print publication:
- September 2022
-
- Article
- Export citation
Asymptotics of the overflow in urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 797-824
- Print publication:
- September 2022
-
- Article
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Coexistence of lazy frogs on
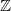 ${\mathbb{Z}}$
${\mathbb{Z}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 702-713
- Print publication:
- September 2022
-
- Article
- Export citation
Logarithmic heavy traffic error bounds in generalized switch and load balancing systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 652-669
- Print publication:
- September 2022
-
- Article
- Export citation