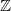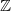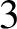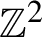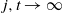Refine listing
Actions for selected content:
1451 results in 60Kxx
Mutually interacting superprocesses with migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 904-929
- Print publication:
- September 2022
-
- Article
- Export citation
Asymptotics of the overflow in urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 797-824
- Print publication:
- September 2022
-
- Article
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Coexistence of lazy frogs on
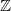 ${\mathbb{Z}}$
${\mathbb{Z}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 702-713
- Print publication:
- September 2022
-
- Article
- Export citation
Logarithmic heavy traffic error bounds in generalized switch and load balancing systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 652-669
- Print publication:
- September 2022
-
- Article
- Export citation
Some results on the telegraph process driven by gamma components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 808-848
- Print publication:
- September 2022
-
- Article
- Export citation
Exponential and gamma form for tail expansions of first-passage distributions in semi-markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1291-1319
- Print publication:
- December 2022
-
- Article
- Export citation
Probability of total domination for transient reflecting processes in a quadrant
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1094-1138
- Print publication:
- December 2022
-
- Article
- Export citation
Subexponential potential asymptotics with applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 783-807
- Print publication:
- September 2022
-
- Article
- Export citation
Normal Approximation for Functions of Hidden Markov Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
The diameter of the uniform spanning tree of dense graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1010-1030
-
- Article
- Export citation
Proper
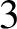 $3$-colorings of
$3$-colorings of 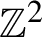 $\mathbb {Z}^{2}$ are Bernoulli
$\mathbb {Z}^{2}$ are Bernoulli
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 27 April 2022, pp. 2002-2027
- Print publication:
- June 2023
-
- Article
- Export citation
KP governs random growth off a 1-dimensional substrate
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 April 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An explicit Dobrushin uniqueness region for Gibbs point processes with repulsive interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 March 2022, pp. 541-555
- Print publication:
- June 2022
-
- Article
- Export citation
An ephemerally self-exciting point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 340-403
- Print publication:
- June 2022
-
- Article
- Export citation
Refined universality for critical KCM: lower bounds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 879-906
-
- Article
- Export citation
SINR percolation for Cox point processes with random powers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 227-253
- Print publication:
- March 2022
-
- Article
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: intermediate generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 421-446
- Print publication:
- June 2022
-
- Article
- Export citation
A stochastic process on a network with connections to Laplacian systems of equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 January 2022, pp. 254-278
- Print publication:
- March 2022
-
- Article
- Export citation
Replica-mean-field limits of fragmentation-interaction-aggregation processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 38-59
- Print publication:
- March 2022
-
- Article
- Export citation