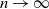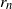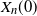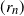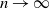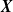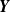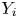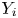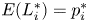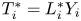Refine listing
Actions for selected content:
1446 results in 60Kxx
Covariances in Pólya urn schemes
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 60-71
-
- Article
- Export citation
Expansion for the critical point of site percolation: the first three terms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 28 September 2021, pp. 430-454
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Soliton Decomposition of the Box-Ball System
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 September 2021, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Gaussian fluctuations of randomly trapped random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 801-838
- Print publication:
- September 2021
-
- Article
- Export citation
Extinction time of the logistic process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 637-676
- Print publication:
- September 2021
-
- Article
- Export citation
An upper bound for the bond percolation threshold of the cubic lattice by a growth process approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 677-692
- Print publication:
- September 2021
-
- Article
- Export citation
Avalanches in a short-memory excitable network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 609-648
- Print publication:
- September 2021
-
- Article
- Export citation
Computing minimal signature of coherent systems through matrix-geometric distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 621-636
- Print publication:
- September 2021
-
- Article
- Export citation
Stochastic properties of generalized finite mixture models with dependent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 794-804
- Print publication:
- September 2021
-
- Article
- Export citation
Controlled branching processes with continuous time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 830-848
- Print publication:
- September 2021
-
- Article
- Export citation
Ordering results for smallest claim amounts from two portfolios of risks with dependent heterogeneous exponentiated location-scale claims
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 1116-1137
-
- Article
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
Sensitivity of mean-field fluctuations in Erlang loss models with randomized routing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 428-448
- Print publication:
- June 2021
-
- Article
- Export citation
Random additions in urns of integers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 335-346
- Print publication:
- June 2021
-
- Article
- Export citation
On classes of life distributions based on the mean time to failure function
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 289-313
- Print publication:
- June 2021
-
- Article
- Export citation
Kelly and Jackson networks with interchangeable, cooperative servers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 463-483
- Print publication:
- June 2021
-
- Article
- Export citation
Continuum line-of-sight percolation on Poisson–Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 510-536
- Print publication:
- June 2021
-
- Article
- Export citation
A product form for the general stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 449-468
- Print publication:
- June 2021
-
- Article
- Export citation
Stochastic analysis of average-based distributed algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 394-410
- Print publication:
- June 2021
-
- Article
- Export citation
Queues with path-dependent arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 484-504
- Print publication:
- June 2021
-
- Article
- Export citation