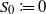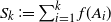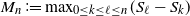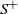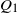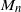Refine listing
Actions for selected content:
1446 results in 60Kxx
STRATEGIC CUSTOMERS IN MARKOVIAN QUEUES WITH VACATIONS AND SYNCHRONIZED ABANDONMENT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 03 July 2020, pp. 89-120
-
- Article
-
- You have access
- Export citation
Representations of component importance for coherent systems with exchangeable components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 385-406
- Print publication:
- June 2020
-
- Article
- Export citation
On two classes of reflected autoregressive processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 657-678
- Print publication:
- June 2020
-
- Article
- Export citation
Stability and moment bounds under utility-maximising service allocations: Finite and infinite networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 463-490
- Print publication:
- June 2020
-
- Article
- Export citation
Long-range orientational order of random near-lattice hard sphere and hard disk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 559-577
- Print publication:
- June 2020
-
- Article
- Export citation
Randomized near-neighbor graphs, giant components and applications in data science
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 458-476
- Print publication:
- June 2020
-
- Article
- Export citation
Tertiles and the time constant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 407-408
- Print publication:
- June 2020
-
- Article
- Export citation
Steady-state analysis of load-balancing algorithms in the sub-Halfin–Whitt regime
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 578-596
- Print publication:
- June 2020
-
- Article
- Export citation
HALF-SPACE MACDONALD PROCESSES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
AN IMPROVED LOWER BOUND FOR THE CRITICAL PARAMETER OF STAVSKAYA’S PROCESS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 May 2020, pp. 517-524
- Print publication:
- December 2020
-
- Article
- Export citation
Directed preferential attachment models: Limiting degree distributions and their tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 122-136
- Print publication:
- March 2020
-
- Article
- Export citation
Long-time behavior of Lévy-driven Ornstein–Uhlenbeck processes with regime switching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 266-279
- Print publication:
- March 2020
-
- Article
- Export citation
Transient analysis for exponential time-limited polling models under the preemptive repeat random policy
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 32-60
- Print publication:
- March 2020
-
- Article
- Export citation
Generalized stacked contact process with variable host fitness
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 97-121
- Print publication:
- March 2020
-
- Article
- Export citation
On the multi-state signatures of ordered system lifetimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 291-318
- Print publication:
- March 2020
-
- Article
- Export citation
Improvements on the distribution of maximal segmental scores in a Markovian sequence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 29-52
- Print publication:
- March 2020
-
- Article
- Export citation
On relative ageing of coherent systems with dependent identically distributed components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 348-376
- Print publication:
- March 2020
-
- Article
- Export citation
A renewal theory approach to two-state switching problems with infinite values
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 1-18
- Print publication:
- March 2020
-
- Article
- Export citation
The existence of a giant cluster for percolation on large Crump–Mode–Jagers trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 266-290
- Print publication:
- March 2020
-
- Article
- Export citation
The potentially negative effects of cooperation in service systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 319-347
- Print publication:
- March 2020
-
- Article
- Export citation