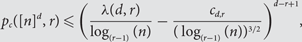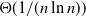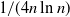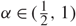Refine listing
Actions for selected content:
1446 results in 60Kxx
An Improved Upper Bound for Bootstrap Percolation in All Dimensions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 17 June 2019, pp. 936-960
-
- Article
- Export citation
A martingale view of Blackwell’s renewal theorem and its extensions to a general counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 602-623
- Print publication:
- June 2019
-
- Article
- Export citation
Reliability analysis of k-out-of-n systems based on a grouping of components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 339-357
- Print publication:
- June 2019
-
- Article
- Export citation
First passage percolation on sparse random graphs with boundary weights
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 458-471
- Print publication:
- June 2019
-
- Article
- Export citation
Transformed Lévy processes as state-dependent wear models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 468-486
- Print publication:
- June 2019
-
- Article
- Export citation
Comparison results for M/G/1 queues with waiting and sojourn time deadlines
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 524-532
- Print publication:
- June 2019
-
- Article
- Export citation
Who is the infector? General multi-type epidemics and real-time susceptibility processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 606-631
- Print publication:
- June 2019
-
- Article
- Export citation
The sharp threshold for jigsaw percolation in random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 378-407
- Print publication:
- June 2019
-
- Article
- Export citation
Renewal processes, population dynamics, and unimodular trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 339-357
- Print publication:
- June 2019
-
- Article
- Export citation
New perspectives on the Erlang-A queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 268-299
- Print publication:
- March 2019
-
- Article
- Export citation
On negative association of some finite point processes on general state spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 139-152
- Print publication:
- March 2019
-
- Article
- Export citation
Exact sampling of the infinite horizon maximum of a random walk over a nonlinear boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 116-138
- Print publication:
- March 2019
-
- Article
- Export citation
Exact simulation of generalised Vervaat perpetuities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 57-75
- Print publication:
- March 2019
-
- Article
- Export citation
Deviation bounds for the first passage time in the frog model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 184-208
- Print publication:
- March 2019
-
- Article
- Export citation
A particle system approach to aggregation phenomena
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 282-306
- Print publication:
- March 2019
-
- Article
- Export citation
Diffusion approximations for load balancing mechanisms in cloud storage systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 41-86
- Print publication:
- March 2019
-
- Article
- Export citation
A Boltzmann Approach to Percolation on Random Triangulations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Occupation times of alternating renewal processes with Lévy applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1287-1308
- Print publication:
- December 2018
-
- Article
- Export citation
Random systems in ultrametric spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 83-97
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
The nonhomogeneous frog model on ℤ
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1093-1112
- Print publication:
- December 2018
-
- Article
- Export citation