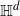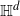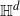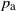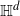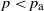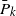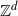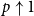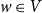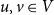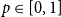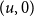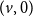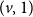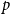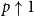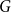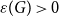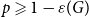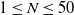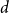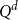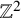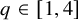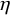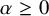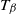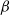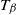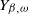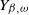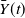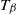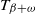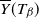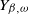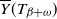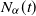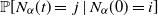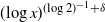Refine listing
Actions for selected content:
1446 results in 60Kxx
SIR epidemics driven by Feller processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1293-1316
- Print publication:
- December 2023
-
- Article
- Export citation
Fluctuations for Some Nonstationary Interacting Particle Systems via Boltzmann–Gibbs Principle
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting shape for first-passage percolation models on random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1367-1385
- Print publication:
- December 2023
-
- Article
- Export citation
Workload analysis of a two-queue fluid polling model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 March 2023, pp. 1003-1030
- Print publication:
- September 2023
-
- Article
- Export citation
Thin-ended clusters in percolation in
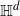 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
On the probability of rumour survival among sceptics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 March 2023, pp. 1096-1111
- Print publication:
- September 2023
-
- Article
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
On some properties of distributions possessing a bathtub-shaped failure rate average
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 January 2023, pp. 693-708
- Print publication:
- June 2023
-
- Article
- Export citation
Local limit theorem for a Markov additive process on
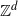 $\mathbb{Z}^d$ with a null recurrent internal Markov chain
$\mathbb{Z}^d$ with a null recurrent internal Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 570-588
- Print publication:
- June 2023
-
- Article
- Export citation
Competing risks and shock models governed by a generalized bivariate Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 709-722
- Print publication:
- June 2023
-
- Article
- Export citation
Reflection principle for finite-velocity random motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 479-492
- Print publication:
- June 2023
-
- Article
- Export citation
The bunkbed conjecture holds in the
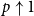 $p\uparrow 1$ limit
$p\uparrow 1$ limit
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 363-369
-
- Article
- Export citation
Global optimisation of the mean first passage time for narrow capture problems in elliptic domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 1269-1287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Supercritical site percolation on the hypercube: small components are small
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal allocation of policy limits in layer reinsurance treaties
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 546-566
-
- Article
- Export citation
Planar random-cluster model: scaling relations
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A decomposition for Lévy processes inspected at Poisson moments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 557-569
- Print publication:
- June 2023
-
- Article
- Export citation
Ruin probabilities in a Markovian shot-noise environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 542-556
- Print publication:
- June 2023
-
- Article
- Export citation
Asymptotic behavior and quasi-limiting distributions on time-fractional birth and death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1199-1227
- Print publication:
- December 2022
-
- Article
- Export citation
Generalizations of forest fires with ignition at the origin
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 24 October 2022, pp. 418-434
- Print publication:
- June 2023
-
- Article
- Export citation