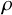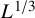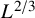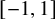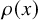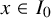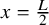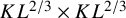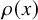Refine listing
Actions for selected content:
1451 results in 60Kxx
Interacting urns on directed networks with node-dependent sampling and reinforcement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 972-996
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spread of an epidemic: a game-theoretic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 January 2025, pp. 749-810
- Print publication:
- September 2025
-
- Article
- Export citation
Mean-field analysis of stochastic networks with reservation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 832-858
- Print publication:
- June 2025
-
- Article
- Export citation
Batch sojourn and delivery times in polling systems on a circle
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 217-242
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moderate deviations of many-server queues via idempotent processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 708-742
- Print publication:
- June 2025
-
- Article
- Export citation
Scaling limit of soliton lengths in a multicolor box-ball system
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution theory for dependent renewal–reward processes and their first-passage times using saddlepoint and residue expansions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 05 December 2024, pp. 447-474
- Print publication:
- June 2025
-
- Article
- Export citation
Exponential decay for constrained-degree percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 795-807
- Print publication:
- June 2025
-
- Article
- Export citation
Convergence of the derivative martingale for the branching random walk in time-inhomogeneous random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 642-676
- Print publication:
- June 2025
-
- Article
- Export citation
Some results on the supremum and on the first passage time of the generalized telegraph process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 453-491
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
First-passage time for Sinai’s random walk in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 29 November 2024, pp. 756-774
- Print publication:
- June 2025
-
- Article
- Export citation
Widths of crossings in Poisson Boolean percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 603-627
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random growth via gradient flow aggregation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 735-755
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extended class of multivariate counting processes and its main properties
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 83-100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expansion of the critical intensity for the random connection model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 November 2024, pp. 158-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On level line fluctuations of SOS surfaces above a wall
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the strong stability of ergodic iterations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 284-297
- Print publication:
- March 2025
-
- Article
- Export citation
On transience of
 $\mathrm{M}/\mathrm{G}/\infty$ queues
$\mathrm{M}/\mathrm{G}/\infty$ queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 572-575
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large-scale particle system with independent jumps and distributed synchronization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 677-707
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A queue with independent and identically distributed arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 319-346
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation






















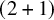
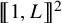 with zero boundary conditions and nonnegative heights (a floor at height
with zero boundary conditions and nonnegative heights (a floor at height 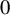
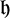
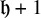
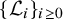
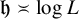
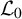
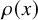
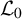
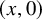
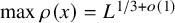
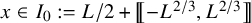 . It is believed that rescaling
. It is believed that rescaling