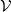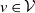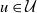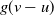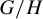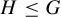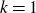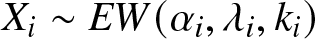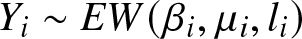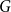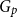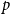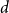Refine listing
Actions for selected content:
1451 results in 60Kxx
A non-homogeneous alternating renewal process model for interval censoring
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 16 September 2024, pp. 494-515
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems of occupation times of normalized binary contact path processes on lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 44-66
- Print publication:
- March 2025
-
- Article
- Export citation
Non-hyperuniformity of Gibbs point processes with short-range interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 August 2024, pp. 1380-1406
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bivariate tempered space-fractional Poisson process and shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1485-1501
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric random intersection graphs with general connection probabilities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1343-1360
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 3385-3427
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ulam–Hammersley problem for multiset permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 09 May 2024, pp. 23-48
- Print publication:
- July 2024
-
- Article
- Export citation
Orderings of extremes among dependent extended Weibull random variables
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 705-732
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multidimensional random motions with a natural number of finite velocities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 1033-1063
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sufficient condition for the quasipotential to be the rate function of the invariant measure of countable-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 960-1003
- Print publication:
- September 2024
-
- Article
- Export citation
Inequalities between time and customer averages for HNB(W)UE arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1199-1219
- Print publication:
- December 2024
-
- Article
- Export citation
Heavy-traffic queue length behavior in a switch under Markovian arrivals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1106-1152
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Analysis of
 ${\textit{d}}$-ary tree algorithms with successive interference cancellation
${\textit{d}}$-ary tree algorithms with successive interference cancellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1075-1105
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration of measure for graphon particle system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1279-1306
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium analysis of the fluid model with two types of parallel customers and incomplete fault
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 12 January 2024, pp. 539-558
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 12 January 2024, pp. 503-538
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Percolation on irregular high-dimensional product graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 377-403
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shock models governed by an inverse gamma mixed Poisson process
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 459-480
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STOCHASTIC MATCHING MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 407-408
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Speed of extinction for continuous-state branching processes in a weakly subcritical Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 886-908
- Print publication:
- September 2024
-
- Article
- Export citation