Refine listing
Actions for selected content:
1446 results in 60Kxx
The Coalescent in Peripatric Metapopulations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 538-557
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Stochastic Order Relations Among Parallel Systems from Weibull Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 102-116
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
A Limit Theorem for a Weiss Epidemic Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 247-257
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Persistence Probability for a Class of Gaussian Processes Related to Random Interface Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 146-163
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Asymptotics of First-Passage Percolation on One-Dimensional Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 182-209
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Error Bounds for Augmented Truncations of Discrete-Time Block-Monotone Markov Chains under Geometric Drift Conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 83-105
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Diffusion-Scale Tightness of Invariant Distributions of a Large-Scale Flexible Service System
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 251-269
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
BRAVO for Many-Server QED Systems with Finite Buffers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 231-250
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Convergence in a Multidimensional Randomized Keynesian Beauty Contest
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 57-82
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Infection Spread in Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-181
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
A Queueing Loss Model with Heterogeneous Skill Based Servers Under Idle Time Ordering Policies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 269-277
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Monotone Cellular Automata in a Random Environment
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 02 February 2015, pp. 687-722
-
- Article
- Export citation
Couplings for locally branching epidemic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 43-56
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Probability Distribution Function for the Euclidean Distance Between Two Telegraph Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1172-1193
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Quasistochastic matrices and Markov renewal theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 359-376
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Characterization of the Generalized Pólya Process and its Applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1148-1171
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On the Conditional Residual Life and Inactivity Time of Coherent Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 990-998
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The naming game in language dynamics revisited
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 139-158
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Two-node fluid network with a heavy-tailed random input: the strong stability case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 249-265
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Dynamic Reliability Modeling of Three-State Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 999-1020
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
 nearest neighbour graph for
nearest neighbour graph for 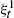 starting with all nodes infected survives up to time
starting with all nodes infected survives up to time