Refine listing
Actions for selected content:
1446 results in 60Kxx
A note on the simulation of the Ginibre point process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1003-1012
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Large deviations for multidimensional state-dependent shot-noise processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1097-1114
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The M/M/c queue with mass exodus and mass arrivals when empty
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 990-1002
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Tollbooth tandem queues with infinite homogeneous servers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 941-961
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Perfect simulation of M/G/c queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1039-1063
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Heavy-traffic limits for polling models with exhaustive service and non-FCFS service order policies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 989-1014
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Conditional Sojourn times and the volatility of payment schemes for bandwidth sharing in packet networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 962-980
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Perfect sampling for infinite server and loss systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 761-786
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A note on the virtual waiting time in the stationary PH/M/c+D queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 899-903
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
The limiting failure rate for a convolution of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 894-898
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Galam's bottom-up hierarchical system and public debate model revisited
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 668-692
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Component importance in coherent systems with exchangeable components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 851-863
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Sharp bounds for exponential approximations under a hazard rate upper bound
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 841-850
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ONE-DIMENSIONAL STOCHASTIC MODELS WITH OPEN BOUNDARIES: INTEGRABILITY, APPLICATIONS AND
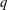 $q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
$q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 520-521
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A Fluid EOQ Model with Markovian Environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 473-489
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Computable Bounds on the Spectral Gap for Unreliable Jackson Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 402-424
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A Recursion Formula for the Moments of the First Passage Time of the Ornstein-Uhlenbeck Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 595-601
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Staffing Many-Server Systems with Admission Control and Retrials
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 450-475
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A Stochastic Failure Model with Dependent Competing Risks and its Applications to Condition-Based Maintenance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 558-573
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Burn-in Procedure Based on a Dependent Covariate Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 506-529
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation