Asymptotic expansions are obtained for the distribution function of a studentized estimator of the offspring mean sequence in an array branching process with immigration. The expansion result is shown to hold in a test function topology. As an application of this result, it is shown that the bootstrapping distribution of the estimator of the offspring mean in a sub-critical branching process with immigration also admits the same expansion (in probability). From these considerations, it is concluded that the bootstrapping distribution provides a better approximation asymptotically than the normal distribution.

In this paper we introduce a quantile dispersion measure. We use it to characterize different classes of ageing distributions. Based on the quantile dispersion measure, we propose a new partial ordering for comparing the spread or dispersion in two probability distributions. This new partial ordering is weaker than the well known dispersive ordering and it retains most of its interesting properties.

We present general criteria for analyzing the crossing characteristics of R I, the reliability function of an m-of-n system of components operating within a laboratory (or test-bench) environment, and R O, the reliability function of the same system now operating subject to an external environment. Inside the laboratory the components' lifetimes may be dependently distributed, and the external environment is modeled using the general approach of Lindley and Singpurwalla (1986). Our techniques, which utilize results basic to the theory of order statistics, apply to broad classes of external environment models.

The dynamical aspects of single channel gating can be modelled by a Markov renewal process, with states aggregated into two classes corresponding to the receptor channel being open or closed, and with brief sojourns in either class not detected. This paper is concerned with the relation between the amount of time, for a given record, in which the channel appears to be open compared to the amount in which it is actually open and the difference in their proportions; this may be used to obtain information on the unobserved actual process from the observed one. Results, with extensions, on exponential families have been applied to obtain relevant generating functions and asymptotic normal distributions, including explicit forms for the parameters. Numerical results are given as illustration in special cases.

It is shown that totally positive order 2 (TP2) properties of the infinitesimal generator of a continuous-time Markov chain with totally ordered state space carry over to the chain's transition distribution function. For chains with such properties, failure rate characteristics of the first passage times are established. For Markov chains with partially ordered state space, it is shown that the first passage times have an IFR distribution under a multivariate total positivity condition on the transition function.

The number of items of data which are irretrievable without additional effort after hashing can be greatly reduced if several hash tables are used simultaneously. Here we show that, in a multiple hashing scheme, this number has a distribution very close to Poisson. Thus choosing the number and sizes of the tables to minimize the expected number of irretrievable items is the right way to dimension a scheme.

We compare R 1(t), the reliability function of a redundant m-of-n system operating within the laboratory, with R D(t), the reliability function of the same system operating subject to environmental effects. Within the laboratory, all component lifetimes are independent and identically distributed according to G(α + 1, λ), a gamma distribution with index α + 1 and scale λ. Outside the laboratory, we adopt the model of Lindley and Singpurwalla (J. Appl. Prob. 23 (1986), 418-431) and assume that, conditional on a positive random variable η which models the effect of the common environment, all component lifetimes are independent and identically distributed according to G(α + 1, λη). When α is a non-negative integer we prove that for R D(t) to underestimate (resp. overestimate) R 1(t) for all t sufficiently close to zero, it is necessary and sufficient that E(η (n-m + 1)(α+1)) > 1 (resp. E(η (n-m + 1)(α+1)) < 1). In the case in which n = 2, m= 1 and α = 0 we obtain a special case of a result of Currit and Singpurwalla (J. Appl. Prob. 26 (1988), 763-771). As an application, we obtain a necessary and sufficient condition under which R D(t) initially understimates (or overestimates) R 1(t) when η follows a gamma or an inverse Gaussian distribution.

Given a two-dimensional Poisson process, X, with intensity λ, we are interested in the largest number of points, L, contained in a translate of a fixed scanning set, C, restricted to lie inside a rectangular area.

The distribution of L is accurately approximated for rectangular scanning sets, using a technique that can be extended to higher dimensions. Reasonable approximations for non-rectangular scanning sets are also obtained using a simple correction of the rectangular result.

A planar graph contains faces which can be classified into types depending on the number of edges on the face boundaries. Under various natural rules for randomly dividing faces by the addition of new edges, we investigate the limiting distribution of face type as the number of divisions increases.

Invariance of a random discrete distribution under size-biased permutation is equivalent to a conjunction of symmetry conditions on its finite-dimensional distributions. This is applied to characterize residual allocation models with independent factors that are invariant under size-biased permutation. Apart from some exceptional cases and minor modifications, such models form a two-parameter family of generalized Dirichlet distributions.

We derive upper bounds for the total variation distance, d, between the distributions of two random sums of non-negative integer-valued random variables. The main results are then applied to some important random sums, including cluster binomial and cluster multinomial distributions, to obtain bounds on approximating them to suitable Poisson or compound Poisson distributions. These bounds are generally better than the known results on Poisson and compound Poisson approximations. We also obtain a lower bound for d and illustrate it with an example.

The series expansion for the solution of the integral equation for the first-passage-time probability density function, obtained by resorting to the fixed point theorem, is used to achieve approximate evaluations for which error bounds are indicated. A different use of the fixed point theorem is then made to determine lower and upper bounds for asymptotic approximations, and to examine their range of validity.

We consider the exact distribution of the number of peaks in a random permutation of the integers 1, 2, ···, n. This arises from a test of whether n successive observations from a continuous distribution are i.i.d. The Eulerian numbers, which figure in the p.g.f., are then shown to provide a link between the simpler problem of ascents (which has been thoroughly analysed) and both our problem of peaks and similar problems on the circle. This link then permits easy deduction of certain general properties, such as linearity in n of the cumulants, in the more complex settings. Since the focus of the paper is on exact distributional results, a uniform bound on the deviation from the limiting normal is included. A secondary purpose of the paper is synthesis, beginning with the more familiar setting of peaks and troughs.

The cumulative distribution of the finite sum of the binary sequence of order k is studied and some of its applications discussed. Certain properties of this sequence are investigated and uniformly superior bounds for the cumulative distribution under minimal information on the ‘success' probabilities are derived.

We first introduce a Lorenz ordering family of distributions which are related to the gamma distribution, and then prove that the weak convergence within this family is equivalent to the convergence of each moment sequence of positive orders to the corresponding moment of the limiting distribution.

Harlow et al. (1983) have given a recursive formula which is fundamental for computing the bundle strength distribution under a general class of load sharing rules called monotone load sharing rules. As the bundle size increases, the formula becomes prohibitively complex and, by itself, does not give much insight into the relationship of the assumed load sharing rule to the overall strength distribution. In this paper, an algorithm is given which gives some additional insight into this relationship. Here it is shown how to explicitly compute the bundle strength survival distribution by using a new type of graph called the loading diagram. The graph is parallel in structure and recursive in nature and so would appear to lend itself to large-scale computation. In addition, the graph has an interesting property (which we refer to as the cancellation property) which is related to the asymptotics of the Weibull as a minimum stable law.

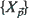Let be a real-valued, homogeneous, and isotropic random field indexed in 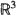. When restricted to those indices 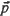with 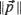, the Euclidean length of 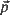, equal to 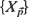r (a positive constant), then the random field resides on the surface of a sphere of radius 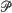r. Using a modified stratified spherical sampling plan (Brown (1993)) on the sphere, define 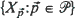to be a realization of the random process and 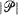to be the cardinality of 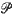. Without specifying the dependence structure of 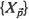nor the marginal distribution of the 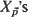, conditions for asymptotic normality of the standardized sample mean, 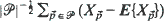, are given. The conditions on 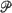and 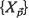are motivated by the ideas and results for dependent stationary sequences.

In this paper we establish a characterization theorem for a general class of life-testing models based on a relationship between conditional expectation and the failure rate function. As a simple application of the theorem, we characterize the gamma, Weibull, and Gompertz distributions, since they have many probabilistic and statistical properties useful in both biometry and engineering reliability.

In the present paper we study the number of occurrences of non-overlapping success runs of length in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.

Consider a sequence of possibly dependent random variables having the same marginal distribution F, whose tail 1−F is regularly varying at infinity with an unknown index − α < 0 which is to be estimated. For i.i.d. data or for dependent sequences with the same marginal satisfying mixing conditions, it is well known that Hill's estimator is consistent for α−1 and asymptotically normally distributed. The purpose of this paper is to emphasize the central role played by the tail empirical process for the problem of consistency. This approach allows us to easily prove Hill's estimator is consistent for infinite order moving averages of independent random variables. Our method also suffices to prove that, for the case of an AR model, the unknown index can be estimated using the residuals generated by the estimation of the autoregressive parameters.