Refine listing
Actions for selected content:
225 results in 62Exx
A martingale characterization of Pólya-Lundberg processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 741-754
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A discrete multivariate distribution resulting from the law of small numbers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-866
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Tail behavior of negatively associated heavy-tailed sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-593
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Limiting dependence structures for tail events, with applications to credit derivatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 563-586
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Asymptotic behavior of a general class of mixture failure rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 244-262
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Exact distribution of word counts in shuffled sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 116-133
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Compound Poisson Approximation Inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 282-288
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Conditional tail expectations for multivariate phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 810-825
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
On increasing-failure-rate random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 797-809
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Asymptotic baseline of the hazard rate function of mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 892-901
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Multiperiod conditional distribution functions for conditionally normal GARCH(1, 1) models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-445
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
On a deposition process on the circle with disorder
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 996-1020
- Print publication:
- December 2004
-
- Article
- Export citation
Path reversal, islands, and the gapped alignment of random sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 975-983
- Print publication:
- December 2004
-
- Article
- Export citation
A study of the Hartman–Watson distribution motivated by numerical problems related to the pricing of Asian options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1058
- Print publication:
- December 2004
-
- Article
- Export citation
Poisson approximation for (k 1, k 2)-events via the Stein-Chen method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1081-1092
- Print publication:
- December 2004
-
- Article
- Export citation
Finite- and infinite-time ruin probabilities in the presence of stochastic returns on investments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1278-1299
- Print publication:
- December 2004
-
- Article
- Export citation
Some properties of ageing notions based on the moment-generating-function order
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 927-934
- Print publication:
- September 2004
-
- Article
- Export citation
Distribution of the amount of genetic material from a chromosomal segment surviving to the following generation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 345-354
- Print publication:
- June 2004
-
- Article
- Export citation
Asymptotic behavior of tail and local probabilities for sums of subexponential random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 108-116
- Print publication:
- March 2004
-
- Article
- Export citation
Asymptotics of the sample mean and sample covariance of long-range-dependent series
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-392
- Print publication:
- 2004
-
- Article
- Export citation
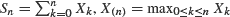 , and
, and 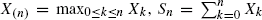 and
and 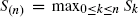 for
for 