Asymptotic independence of the components of random vectors is a concept used in many applications. The standard criteria for checking asymptotic independence are given in terms of distribution functions (DFs). DFs are rarely available in an explicit form, especially in the multivariate case. Often we are given the form of the density or, via the shape of the data clouds, we can obtain a good geometric image of the asymptotic shape of the level sets of the density. In this paper we establish a simple sufficient condition for asymptotic independence for light-tailed densities in terms of this asymptotic shape. This condition extends Sibuya's classic result on asymptotic independence for Gaussian densities.

Consider a sequence of exchangeable or independent binary trials ordered on a line or on a circle. The statistics denoting the number of times an F-S string of length (at least) k1 + k2, that is, (at least) k1 failures followed by (at least) k2 successes in n such trials, are studied. The associated waiting time for the rth occurrence of an F-S string of length (at least) k1 + k2 in linearly ordered trials is also examined. Exact formulae, lower/upper bounds and approximations are derived for their distributions. Mean values and variances of the number of occurrences of F-S strings are given in exact formulae too. Particular exchangeable and independent sequences of binary random variables, used in applied research, combined with numerical examples clarify further the theoretical results.

We consider a nearly unstable, or near unit root, AR(1) process with regularly varying innovations. Two different approximations for the stationary distribution of such processes exist: a Gaussian approximation arising from the nearly unstable nature of the process and a heavy-tail approximation related to the tail asymptotics of the innovations. We combine these two approximations to obtain a new uniform approximation that is valid on the entire real line. As a corollary, we obtain a precise description of the regions where each of the Gaussian and heavy-tail approximations should be used.

We apply Stein's method for probabilistic approximation by a compound geometric distribution, with applications to Markov chain hitting times and sequence patterns. Bounds on our Stein operator are found using a complex analytical approach based on generating functions and Cauchy's formula.

A necessary condition for a rational Laplace–Stieltjes transform to correspond to a matrix exponential distribution is that the pole of maximal real part is real and negative. Given a rational Laplace–Stieltjes transform with such a pole, we present a method to determine whether or not the numerator polynomial admits a transform that corresponds to a matrix exponential distribution. The method relies on the minimization of a continuous function of one variable over the nonnegative real numbers. Using this approach, we give an alternative characterization for all matrix exponential distributions of order three.

A model for describing the lifetimes of coherent systems, where the failures of components may have an impact on the lifetimes of the remaining components, is proposed. The model is motivated by the definition of sequential order statistics (cf. Kamps (1995)). Sequential order statistics describe the successive failure times in a sequential k-out-of-n system, where the distribution of the remaining components' lifetimes is allowed to change after every failure of a component. In the present paper, general component lifetimes which can be influenced by failures are considered. The ordered failure times of these components can be used to extend the concept of sequential order statistics. In particular, a definition of sequential order statistics based on exchangeable components is proposed. By utilizing the system signature (cf. Samaniego (2007)), the distribution of the lifetime of a coherent system with failure-dependent exchangeable component lifetimes is shown to be given by a mixture of the distributions of sequential order statistics. Furthermore, some results on the joint distribution of sequential order statistics based on exchangeable components are given.

In this paper we are concerned with the equilibrium distribution ∏n of the nth element in a sequence of continuous-time density-dependent Markov processes on the integers. Under a (2+α)th moment condition on the jump distributions, we establish a bound of order O(n-(α+1)/2√logn) on the difference between the point probabilities of ∏n and those of a translated Poisson distribution with the same variance. Except for the factor √logn, the result is as good as could be obtained in the simpler setting of sums of independent, integer-valued random variables. Our arguments are based on the Stein-Chen method and coupling.

In this paper, a stochastic integral of Ornstein–Uhlenbeck type is represented to be the sum of two independent random variables: one has a tempered stable distribution and the other has a compound Poisson distribution. In distribution, the compound Poisson random variable is equal to the sum of a Poisson-distributed number of positive random variables, which are independent and identically distributed and have a common specified density function. Based on the representation of the stochastic integral, we prove that the transition distribution of the tempered stable Ornstein–Uhlenbeck process is self-decomposable and that the transition density is a C∞-function.

In this paper we refine a Poisson limit theorem of Gnedenko and Kolmogorov (1954): we determine the error order of a Poisson approximation for sums of asymptotically negligible integer-valued random variables that converge in distribution to the Poisson law. As an application of our results, we investigate the case of the coupon collector's problem when the distribution of the collector's waiting time is asymptotically Poisson.

We study the convolution of compound negative binomial distributions with arbitrary parameters. The exact expression and also a random parameter representation are obtained. These results generalize some recent results in the literature. An application of these results to insurance mathematics is discussed. The sums of certain dependent compound Poisson variables are also studied. Using the connection between negative binomial and gamma distributions, we obtain a simple random parameter representation for the convolution of independent and weighted gamma variables with arbitrary parameters. Applications to the reliability of m-out-of-n:G systems and to the shortest path problem in graph theory are also discussed.

Let X1, X2,… and Y1, Y2,… be two sequences of absolutely continuous, independent and identically distributed (i.i.d.) random variables with equal means E(Xi)=E(Yi), i=1,2,… In this work we provide upper bounds for the total variation and Kolmogorov distances between the distributions of the partial sums ∑i=1nXi and ∑i=1nYi. In the case where the distributions of the Xis and the Yis are compared with respect to the convex order, the proposed upper bounds are further refined. Finally, in order to illustrate the applicability of the results presented, we consider specific examples concerning gamma and normal approximations.

Recently, Makri, Philippou and Psillakis (2007b) studied the exact distribution of success run statistics defined on an urn model. They derived the exact distributions of various success run statistics for a sequence of binary trials generated by the Pólya-Eggenberger sampling scheme. In our study we derive the joint distributions of run statistics defined on the multicolor urn model using a simple unified combinatorial approach and extend some of the results of Makri, Philippou and Psillakis (2007b). As a consequence of our results, we obtain the joint distributions of success and failure runs defined on the two-color urn model. The results enable us to compute the characteristics of particular consecutive-type systems and start-up demonstration tests.

Throughout recent years, various sequential Monte Carlo methods, i.e. particle filters, have been widely applied to various applications involving the evaluation of the generally intractable stochastic discrete-time filter. Although convergence results exist for finite-time intervals, a stronger form of convergence, namely, uniform convergence, is required for bounding the error on an infinite-time interval. In this paper we prove easily verifiable conditions for the filter applications that are sufficient for the uniform convergence of certain particle filters. Essentially, the conditions require the observations to be accurate enough. No mixing or ergodicity conditions are imposed on the signal process.

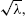We present a method to obtain both exact values and sharp estimates for the total variation distance between binomial and Poisson distributions with the same mean λ. We give a simple efficient algorithm, whose complexity order is to compute exact values. Such an algorithm can be further simplified for moderate sample sizes 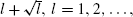n, provided that λ is neither close to from the left nor close to 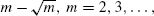from the right. Sharp estimates, better than other known estimates in the literature, are also provided. The 0s of the second Krawtchouk and Charlier polynomials play a fundamental role.

Detection of repeated sequences within complete genomes is a powerful tool to help understanding genome dynamics and species evolutionary history. To distinguish significant repeats from those that can be obtained just by chance, statistical methods have to be developed. In this paper we show that the distribution of the number of long repeats in long sequences generated by stationary Markov chains can be approximated by a Poisson distribution with explicit parameter. Thanks to the Chen-Stein method we provide a bound for the approximation error; this bound converges to 0 as soon as the length n of the sequence tends to ∞ and the length t of the repeats satisfies n2ρt = O(1) for some 0 < ρ < 1. Using this Poisson approximation, p-values can then be easily calculated to determine if a given genome is significantly enriched in repeats of length t.

This paper presents new Gaussian approximations for the cumulative distribution function P(Aλ ≤ s) of a Poisson random variable Aλ with mean λ. Using an integral transformation, we first bring the Poisson distribution into quasi-Gaussian form, which permits evaluation in terms of the normal distribution function Φ. The quasi-Gaussian form contains an implicitly defined function y, which is closely related to the Lambert W-function. A detailed analysis of y leads to a powerful asymptotic expansion and sharp bounds on P(Aλ ≤ s). The results for P(Aλ ≤ s) differ from most classical results related to the central limit theorem in that the leading term Φ(β), with is replaced by Φ(α), where α is a simple function of s that converges to β as s tends to ∞. Changing β into α turns out to increase precision for small and moderately large values of s. The results for P(Aλ ≤ s) lead to similar results related to the Erlang B formula. The asymptotic expansion for Erlang's B is shown to give rise to accurate approximations; the obtained bounds seem to be the sharpest in the literature thus far.

In this paper we study the asymptotic tail probabilities of sums of subexponential, nonnegative random variables, which are dependent according to certain general structures with tail independence. The results show that the subexponentiality of the summands eliminates the impact of the dependence on the tail behavior of the sums.

We make a correction to an important result by Cline [D. B. H. Cline, ‘Convolutions of distributions with exponential tails’, J. Austral. Math. Soc. (Series A)43 (1987), 347–365; D. B. H. Cline, ‘Convolutions of distributions with exponential tails: corrigendum’, J. Austral. Math. Soc. (Series A)48 (1990), 152–153] on the closure of the exponential class under convolution power mixtures (random summation).

Aven and Jensen (1999) proposed an approximation to the downtime distribution for arbitrary coherent systems with binary and independent repairable components, where each component follows an alternating renewal process. The approximation is based on a mixture of the duration distributions of the cut sets in the system. We extend this approach to coherent systems composed by multistate independent components, where every component follows a semi-Markov process and where we introduce the concept of a minimal cut set in the multistate setting. We test our proposal on a simple power demand-generation system, by comparing the analytic approximation with simulation results, and we find it is accurate when the system is highly available.

Statistics denoting the numbers of success runs of length exactly equal and at least equal to a fixed length, as well as the sum of the lengths of success runs of length greater than or equal to a specific length, are considered. They are defined on both linearly and circularly ordered binary sequences, derived according to the Pólya-Eggenberger urn model. A waiting time associated with the sum of lengths statistic in linear sequences is also examined. Exact marginal and joint probability distribution functions are obtained in terms of binomial coefficients by a simple unified combinatorial approach. Mean values are also derived in closed form. Computationally tractable formulae for conditional distributions, given the number of successes in the sequence, useful in nonparametric tests of randomness, are provided. The distribution of the length of the longest success run and the reliability of certain consecutive systems are deduced using specific probabilities of the studied statistics. Numerical examples are given to illustrate the theoretical results.