Refine listing
Actions for selected content:
225 results in 62Exx
Error bounds for augmented truncation approximations of Markov chains via the perturbation method
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 645-669
- Print publication:
- June 2018
-
- Article
- Export citation
Exact moderate and large deviations for linear random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 431-449
- Print publication:
- June 2018
-
- Article
- Export citation
On the significands of uniform random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 353-367
- Print publication:
- June 2018
-
- Article
- Export citation
On the age of a randomly picked individual in a linear birth-and-death process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 82-93
- Print publication:
- March 2018
-
- Article
- Export citation
A necessary and sufficient condition for the subexponentiality of the product convolution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 57-73
- Print publication:
- March 2018
-
- Article
- Export citation
Poisson-saddlepoint approximation for Gibbs point processes with infinite-order interaction: in memory of Peter Hall
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1008-1026
- Print publication:
- December 2017
-
- Article
- Export citation
Asymptotic failure rates for a general class of frailty models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1230-1259
- Print publication:
- December 2017
-
- Article
- Export citation
Taylor's law, via ratios, for some distributions with infinite mean
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 657-669
- Print publication:
- September 2017
-
- Article
- Export citation
Multiplicative Noise Removal Based on Unbiased Box-Cox Transformation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 803-828
- Print publication:
- September 2017
-
- Article
- Export citation
NOVEL PREPROCESSING APPROACHES FOR OMICS DATA TYPES AND THEIR PERFORMANCE EVALUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 348-349
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Asymptotic results for the multiple scan statistic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 320-330
- Print publication:
- March 2017
-
- Article
- Export citation
Corrected discrete approximations for the conditional and unconditional distributions of the continuous scan statistic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 304-319
- Print publication:
- March 2017
-
- Article
- Export citation
The limit distribution of the largest interpoint distance for distributions supported by ad-dimensional ellipsoid and generalizations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1256-1270
- Print publication:
- December 2016
-
- Article
- Export citation
MODELLING AND SIMULATION OF VOLUMETRIC RAINFALL FOR A CATCHMENT IN THE MURRAY–DARLING BASIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 08 September 2016, pp. 119-142
-
- Article
-
- You have access
- Export citation
Compound geometric approximation under a failure rate constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 700-714
- Print publication:
- September 2016
-
- Article
- Export citation
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 28 June 2016, e17
-
- Article
-
- You have access
- Open access
- Export citation
The DFR Property for Counting Processes Stopped at an Independent Random Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 574-585
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Infection Spread in Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-181
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Improved Approximation of the Sum of Random Vectors by the Skew Normal Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 466-482
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On the Joint Distribution of Stopping Times and Stopped Sums in Multistate Exchangeable Trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 483-491
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
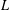
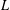
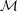
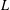


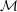
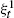 starting with all nodes infected survives up to time
starting with all nodes infected survives up to time 