Refine listing
Actions for selected content:
225 results in 62Exx
Size-and-shape distributions for paired landmark data
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 893-905
- Print publication:
- December 1994
-
- Article
- Export citation
Classes of life distributions and renewal counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1110-1115
- Print publication:
- December 1994
-
- Article
- Export citation
The Integrated Cauchy Functional Equation: Some Comments on Recent Papers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 825-829
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Approximating gamma distributions by normalized negative binomial distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 1994
-
- Article
- Export citation
An unreliable server characterization of the exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 274-279
- Print publication:
- March 1994
-
- Article
- Export citation
Asymptotic Properties of Estimators for the Parameters of Spatial Inhomogeneous Poisson Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 122-154
- Print publication:
- March 1994
-
- Article
- Export citation
The variance of a truncated mixed exponential process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 167-179
- Print publication:
- March 1994
-
- Article
- Export citation
A Note on Electrical Networks and the Inverse Gaussian Distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-67
- Print publication:
- March 1994
-
- Article
- Export citation
Poisson approximations for the distribution and moments of ordered m-spacings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 271-281
- Print publication:
- 1994
-
- Article
- Export citation
Compound poisson approximations for the numbers of extreme spacings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 847-874
- Print publication:
- December 1993
-
- Article
- Export citation
Some characterizations of the exponential and geometric distributions arising in a queueing system with an unreliable server
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 985-990
- Print publication:
- December 1993
-
- Article
- Export citation
Sums and maxima of discrete stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 863-876
- Print publication:
- December 1993
-
- Article
- Export citation
The probability that the largest observation is censored
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 602-615
- Print publication:
- September 1993
-
- Article
- Export citation
Bivariate life distributions from Pólya's urn model for contagion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 497-508
- Print publication:
- September 1993
-
- Article
- Export citation
Some characterizations of exponential or geometric distributions in a non-stationary record value model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 373-381
- Print publication:
- June 1993
-
- Article
- Export citation
Some characterizations of the Poisson process and geometric renewal process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 121-130
- Print publication:
- March 1993
-
- Article
- Export citation
On distributions having the almost-lack-of-memory property
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 691-698
- Print publication:
- September 1992
-
- Article
- Export citation
Dependence structure of Poisson-paced records
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-596
- Print publication:
- September 1992
-
- Article
- Export citation
On ratios of random variables and generalised mortality rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 268-279
- Print publication:
- June 1992
-
- Article
- Export citation
Exact distribution theory for some point process record models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 20-44
- Print publication:
- March 1992
-
- Article
- Export citation
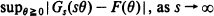 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 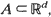 , with intensity function
, with intensity function 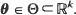 . In this article, we show that the maximum likelihood estimator
. In this article, we show that the maximum likelihood estimator 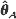 and the Bayes estimator
and the Bayes estimator 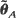 are consistent, asymptotically normal, and asymptotically efficient as the sample region
are consistent, asymptotically normal, and asymptotically efficient as the sample region  . These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0,
. These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0, 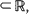 , where
, where 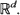 . Furthermore, a Cramér–Rao lower bound is found for any estimator
. Furthermore, a Cramér–Rao lower bound is found for any estimator 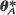 of
of 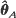 and
and 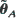 are considered for modulated (Cox (1972)), and linear Poisson processes.
are considered for modulated (Cox (1972)), and linear Poisson processes.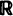 and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be
and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be 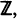 any c.d.f.
any c.d.f. 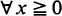 is an admissible solution coinciding with
is an admissible solution coinciding with 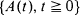 , with
, with 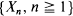 the sequence of interarrival times. We prove that, given a function
the sequence of interarrival times. We prove that, given a function 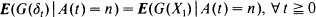 holds for a single positive integer
holds for a single positive integer 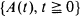 is a Poisson process. On the other hand, for a delayed renewal process
is a Poisson process. On the other hand, for a delayed renewal process 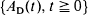 with
with 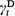 the residual life at
the residual life at 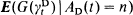 is independent of
is independent of 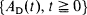 is an arbitrarily delayed Poisson process. We also give some corresponding results about characterizing the common distribution function
is an arbitrarily delayed Poisson process. We also give some corresponding results about characterizing the common distribution function 