Refine listing
Actions for selected content:
225 results in 62Exx
Characterizations of classes of lifetime distributions generalizing the NBUE class
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 20-32
- Print publication:
- March 2003
-
- Article
- Export citation
On the distance between the distributions of random sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 87-106
- Print publication:
- March 2003
-
- Article
- Export citation
Sooner and later waiting time problems for patterns in Markov dependent trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-86
- Print publication:
- March 2003
-
- Article
- Export citation
Distribution of the number of words with a prescribed frequency and tests of randomness
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 775-797
- Print publication:
- December 2002
-
- Article
- Export citation
A family of densities derived from the three-parameter Dirichlet process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 764-774
- Print publication:
- December 2002
-
- Article
- Export citation
Error bounds on multivariate Normal approximations for word count statistics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 559-586
- Print publication:
- September 2002
-
- Article
- Export citation
Matrix-variate Kummer-Beta distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-26
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
On the distance between convex-ordered random variables, with applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 349-374
- Print publication:
- June 2002
-
- Article
- Export citation
On the behaviour of some new ageing properties based upon the residual life of k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-433
- Print publication:
- June 2002
-
- Article
- Export citation
Classification and lumpability in the stochastic Hopfield model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 19 February 2016, pp. 930-943
- Print publication:
- December 2001
-
- Article
- Export citation
A note on stochastic comparisons of excess lifetimes of renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 747-753
- Print publication:
- September 2001
-
- Article
- Export citation
Calculation of noncrossing probabilities for Poisson processes and its corollaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 702-716
- Print publication:
- September 2001
-
- Article
- Export citation
Last passage times of minimum contrast estimators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Remarks on converse Carleman and Krein criteria for the classical moment problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-104
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Multivariate product-type lower bounds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-420
- Print publication:
- June 2001
-
- Article
- Export citation
Compound Poisson approximation for long increasing sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 449-463
- Print publication:
- June 2001
-
- Article
- Export citation
On the nature of the binomial distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 36-44
- Print publication:
- March 2001
-
- Article
- Export citation
Some new results involving the NBU(2) class of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 242-247
- Print publication:
- March 2001
-
- Article
- Export citation
Stein factor bounds for random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1181-1187
- Print publication:
- December 2000
-
- Article
- Export citation
A use of the Stein-Chen method in time series analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1129-1136
- Print publication:
- December 2000
-
- Article
- Export citation
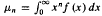 satisfying
satisfying 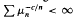 implies that
implies that