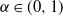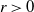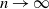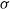Refine listing
Actions for selected content:
225 results in 62Exx
On reconsidering entropies and divergences and their cumulative counterparts: Csiszár's, DPD's and Fisher's type cumulative and survival measures
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 294-321
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How a probabilistic analogue of the mean value theorem yields stein-type covariance identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 350-365
- Print publication:
- June 2022
-
- Article
- Export citation
A generalised Dickman distribution and the number of species in a negative binomial process model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 370-399
- Print publication:
- June 2021
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Normal approximation for mixtures of normal distributions and the evolution of phenotypic traits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 162-188
- Print publication:
- March 2021
-
- Article
- Export citation
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
- Print publication:
- September 2020
-
- Article
- Export citation
Explicit asymptotics on first passage times of diffusion processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 681-704
- Print publication:
- June 2020
-
- Article
- Export citation
Efficient simulation of Lévy-driven point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 927-966
- Print publication:
- December 2019
-
- Article
- Export citation
LOG-CONCAVITY OF COMPOUND DISTRIBUTIONS WITH APPLICATIONS IN OPERATIONAL AND ACTUARIAL MODELS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 23 August 2019, pp. 210-235
-
- Article
- Export citation
Measures of ageing tendency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 358-383
- Print publication:
- June 2019
-
- Article
- Export citation
Moment bounds of PH distributions with infinite or finite support based on the steepest increase property
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 168-183
- Print publication:
- March 2019
-
- Article
- Export citation
Cramér type moderate deviations for random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 223-245
- Print publication:
- March 2019
-
- Article
- Export citation
A conditional Berry–Esseen inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 76-90
- Print publication:
- March 2019
-
- Article
- Export citation
Uniform decomposition of probability measures: quantization, clustering and rate of convergence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1037-1045
- Print publication:
- December 2018
-
- Article
- Export citation
SOME NEW BOUNDS AND APPROXIMATIONS ON TAIL PROBABILITIES OF THE POISSON AND OTHER DISCRETE DISTRIBUTIONS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 11 October 2018, pp. 53-71
-
- Article
- Export citation
Compound Poisson approximation of subgraph counts in stochastic block models with multiple edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 759-782
- Print publication:
- September 2018
-
- Article
- Export citation
Relaxation of monotone coupling conditions: Poisson approximation and beyond
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 742-759
- Print publication:
- September 2018
-
- Article
- Export citation
Kesten's bound for subexponential densities on the real line and its multi-dimensional analogues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 373-395
- Print publication:
- June 2018
-
- Article
- Export citation
Approximation of the difference of two Poisson-like counts by Skellam
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 416-430
- Print publication:
- June 2018
-
- Article
- Export citation