Refine listing
Actions for selected content:
246 results in 62Mxx
The Rao–Blackwell theorem in stereology and some counterexamples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 2-19
- Print publication:
- March 1995
-
- Article
- Export citation
Approximations and boundary conditions for continuous-time threshold autoregressive processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1103-1109
- Print publication:
- December 1994
-
- Article
- Export citation
The Representation and Decomposition of Integrated Stationary Time Series
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 799-819
- Print publication:
- September 1994
-
- Article
- Export citation
Markov Chains in Many Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 756-774
- Print publication:
- September 1994
-
- Article
- Export citation
On Cowan and Mecke's Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 554-560
- Print publication:
- June 1994
-
- Article
- Export citation
On a distributional bound arising in autoregressive model fitting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 401-408
- Print publication:
- June 1994
-
- Article
- Export citation
Asymptotic properties of estimators for parameters of the Boolean model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 301-323
- Print publication:
- June 1994
-
- Article
- Export citation
A reversibility relationship for two Markovian time series models by stationary exponential tailed distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 575-581
- Print publication:
- June 1994
-
- Article
- Export citation
Asymptotic Properties of Estimators for the Parameters of Spatial Inhomogeneous Poisson Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 122-154
- Print publication:
- March 1994
-
- Article
- Export citation
Multivariate self-similar processes: second-order theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-147
- Print publication:
- March 1994
-
- Article
- Export citation
On the solution of Kac-type partial differential equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 311-324
- Print publication:
- 1994
-
- Article
- Export citation
On estimating the diffusion coefficient from discrete observations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 790-804
- Print publication:
- December 1993
-
- Article
- Export citation
Sums and maxima of discrete stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 863-876
- Print publication:
- December 1993
-
- Article
- Export citation
Properties of the spatial unilateral first-order ARMA model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 631-648
- Print publication:
- September 1993
-
- Article
- Export citation
First-order autoregressive logistic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 467-470
- Print publication:
- June 1993
-
- Article
- Export citation
The first-order autoregressive Mittag–Leffler process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 462-466
- Print publication:
- June 1993
-
- Article
- Export citation
Linnik distributions and processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 330-340
- Print publication:
- June 1993
-
- Article
- Export citation
Tail behaviour of the stationary density of general non-linear autoregressive processes of order 1
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 315-329
- Print publication:
- June 1993
-
- Article
- Export citation
Alternating projections and interpolation of stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 921-931
- Print publication:
- December 1992
-
- Article
- Export citation
Uniformly distributed first-order autoregressive time series models and multiplicative congruential random number generators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 896-903
- Print publication:
- December 1992
-
- Article
- Export citation
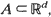 , with intensity function
, with intensity function 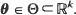 . In this article, we show that the maximum likelihood estimator
. In this article, we show that the maximum likelihood estimator 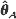 and the Bayes estimator
and the Bayes estimator 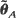 are consistent, asymptotically normal, and asymptotically efficient as the sample region
are consistent, asymptotically normal, and asymptotically efficient as the sample region  . These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0,
. These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0, 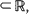 , where
, where 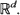 . Furthermore, a Cramér–Rao lower bound is found for any estimator
. Furthermore, a Cramér–Rao lower bound is found for any estimator 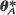 of
of 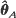 and
and  are considered for modulated (Cox (1972)), and linear Poisson processes.
are considered for modulated (Cox (1972)), and linear Poisson processes.