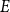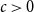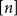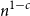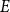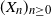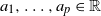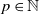Refine search
Actions for selected content:
52341 results in Statistics and Probability
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation
References to R Packages
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 508-513
-
- Chapter
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
Analysis and forecasting of syphilis trends in mainland China based on hybrid time series models
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model and algorithm for pharmaceutical distribution routing problem considering customer priority and carbon emissions
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
International travel as a risk factor for gastrointestinal infections in residents of North East England
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large cryptosporidiosis outbreak associated with an animal contact event in England: a retrospective cohort study, 2023
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1463-1484
- Print publication:
- December 2024
-
- Article
- Export citation
Guiding prevention initiatives by applying network analysis to systems maps of adverse childhood experiences and adolescent suicide
-
- Journal:
- Network Science / Volume 12 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 234-260
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix C - Coupling and Total Variation
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 370-373
-
- Chapter
- Export citation
6 - Bounded Harmonic functions
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 196-245
-
- Chapter
- Export citation
Appendix B - Entropy
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 365-369
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp xv-xvi
-
- Chapter
- Export citation
9 - Gromov’s Theorem
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 301-354
-
- Chapter
- Export citation
Index
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 378-382
-
- Chapter
- Export citation
Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 1-2
-
- Chapter
- Export citation
Preface
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp xi-xiv
-
- Chapter
- Export citation
Bivariate tempered space-fractional Poisson process and shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1485-1501
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - The Milnor–Wolf Theorem
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 273-300
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp i-vi
-
- Chapter
- Export citation