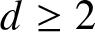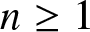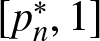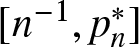Refine search
Actions for selected content:
52343 results in Statistics and Probability
4 - Evaluation of Predictive Models
- from Part I - Framework for Multivariate Biomarker Discovery
-
- Book:
- Multivariate Biomarker Discovery
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp 44-75
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Multivariate Biomarker Discovery
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp xvii-xviii
-
- Chapter
- Export citation
Index
-
- Book:
- Multivariate Biomarker Discovery
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp 273-276
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Multivariate Biomarker Discovery
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp iv-iv
-
- Chapter
- Export citation
On the probability of a Pareto record
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 752-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Advancing digital healthcare engineering for aging ships and offshore structures: an in-depth review and feasibility analysis
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 03 June 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persistence of spectral projections for stochastic operators on large tensor products
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-14
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Risk of central line-associated bloodstream infections during COVID-19 pandemic in intensive care patients in a tertiary care centre in Saudi Arabia
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 03 June 2024, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal experiment design with adjoint-accelerated Bayesian inference
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 31 May 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IDENTIFICATION AND STATISTICAL DECISION THEORY
-
- Journal:
- Econometric Theory / Volume 41 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 977-993
-
- Article
- Export citation
SPURIOUS FACTORS IN DATA WITH LOCAL-TO-UNIT ROOTS
-
- Journal:
- Econometric Theory / Volume 41 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 779-816
-
- Article
- Export citation
Optimizing insurance risk assessment: a regression model based on a risk-loaded approach
-
- Journal:
- Annals of Actuarial Science / Volume 19 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 May 2024, pp. 82-95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPLICATIONS OF FUNCTIONAL DEPENDENCE TO SPATIAL ECONOMETRICS
-
- Journal:
- Econometric Theory , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-36
-
- Article
- Export citation

Multivariate Biomarker Discovery
- Data Science Methods for Efficient Analysis of High-Dimensional Biomedical Data
-
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024
Preface
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xiii-xvi
-
- Chapter
- Export citation
1 - Learning from Data, and Tools for the Task
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-87
-
- Chapter
-
- You have access
- Export citation
3 - Multiple Linear Regression
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 144-207
-
- Chapter
- Export citation
9 - Multivariate Data Exploration and Discrimination
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 400-468
-
- Chapter
- Export citation
Contents
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp vii-x
-
- Chapter
- Export citation
Figures
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xi-xvi
-
- Chapter
- Export citation