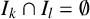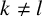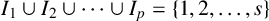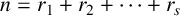FirstView articles
Contents
Research Article
ON A PROBLEM OF NATHANSON ON NONMINIMAL ADDITIVE COMPLEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2025, pp. 1-8
-
- Article
- Export citation
HALPHEN AND THE ELLIPTIC FUNCTIONS OF DU VAL
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ORDERS OF ZEROS OF STRONGLY MONOLITHIC CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-8
-
- Article
- Export citation
PhD Abstract
SPATIAL STATISTICAL INFERENCE FROM A DECISION-THEORETIC VIEWPOINT WITH APPLICATION TO NON-GAUSSIAN ENVIRONMENTAL DATA
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
NOTES ON GENERALISED INTEGRAL POLYNOMIAL PELL EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-13
-
- Article
- Export citation
DERANGEMENTS IN PERMUTATION GROUPS WITH TWO ORBITS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI
 $?$-FUNCTION
$?$-FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-6
-
- Article
- Export citation
GENERALISED MAZUR’S GROWTH NUMBER CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SOME QUADRATICS AND CUBICS OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NORMALISERS OF ALL NON-p-NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-8
-
- Article
- Export citation
PhD Abstract
TRACE FORMULAS IN NONCOMMUTATIVE GEOMETRY
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum
ON THE BURES METRIC,
 $C^*$-NORM AND QUANTUM METRIC - CORRIGENDUM
$C^*$-NORM AND QUANTUM METRIC - CORRIGENDUM
-
- Published online by Cambridge University Press:
- 20 November 2025, p. 1
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
SUMS OF KLOOSTERMAN SUMS OVER SQUARE-FREE AND SMOOTH INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUMS OF SQUARES OF INTEGERS EXCEPT FOR A FIXED ONE
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-11
-
- Article
- Export citation
ON THE GENERALISED SQUEEZING FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE OPEN MAPPINGS OF LOCALLY COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-8
-
- Article
- Export citation
ON THE SHORTEST DISTANCE BETWEEN ORBITS IN CONFORMAL ITERATED FUNCTION SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-11
-
- Article
- Export citation
A NOTE ON GROUPS WITH FINITENESS CONDITIONS ON COMMUTATOR SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-9
-
- Article
- Export citation
ON ADDITIVE COMPLEMENTS IN THE COMPLEMENT OF A SET OF NATURAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-13
-
- Article
- Export citation
ON THE LARGEST PRIME DIVISOR OF n! + 1
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation