In this paper, we construct several new permutation polynomials over finite fields. First, using the linearised polynomials, we construct the permutation polynomial of the form 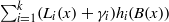 ${ \mathop{\sum }\nolimits}_{i= 1}^{k} ({L}_{i} (x)+ {\gamma }_{i} ){h}_{i} (B(x))$ over
${ \mathop{\sum }\nolimits}_{i= 1}^{k} ({L}_{i} (x)+ {\gamma }_{i} ){h}_{i} (B(x))$ over 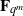 ${\mathbf{F} }_{{q}^{m} } $, where
${\mathbf{F} }_{{q}^{m} } $, where 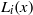 ${L}_{i} (x)$ and
${L}_{i} (x)$ and 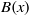 $B(x)$ are linearised polynomials. This extends a theorem of Coulter, Henderson and Matthews. Consequently, we generalise a result of Marcos by constructing permutation polynomials of the forms
$B(x)$ are linearised polynomials. This extends a theorem of Coulter, Henderson and Matthews. Consequently, we generalise a result of Marcos by constructing permutation polynomials of the forms 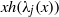 $xh({\lambda }_{j} (x))$ and
$xh({\lambda }_{j} (x))$ and 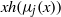 $xh({\mu }_{j} (x))$, where
$xh({\mu }_{j} (x))$, where 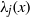 ${\lambda }_{j} (x)$ is the
${\lambda }_{j} (x)$ is the 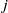 $j$th elementary symmetric polynomial of
$j$th elementary symmetric polynomial of 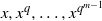 $x, {x}^{q} , \ldots , {x}^{{q}^{m- 1} } $ and
$x, {x}^{q} , \ldots , {x}^{{q}^{m- 1} } $ and 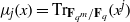 ${\mu }_{j} (x)= {\mathrm{Tr} }_{{\mathbf{F} }_{{q}^{m} } / {\mathbf{F} }_{q} } ({x}^{j} )$. This answers an open problem raised by Zieve in 2010. Finally, by using the linear translator, we construct the permutation polynomial of the form
${\mu }_{j} (x)= {\mathrm{Tr} }_{{\mathbf{F} }_{{q}^{m} } / {\mathbf{F} }_{q} } ({x}^{j} )$. This answers an open problem raised by Zieve in 2010. Finally, by using the linear translator, we construct the permutation polynomial of the form 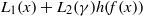 ${L}_{1} (x)+ {L}_{2} (\gamma )h(f(x))$ over
${L}_{1} (x)+ {L}_{2} (\gamma )h(f(x))$ over 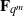 ${\mathbf{F} }_{{q}^{m} } $, which extends a result of Kyureghyan.
${\mathbf{F} }_{{q}^{m} } $, which extends a result of Kyureghyan.
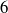 $6$
$6$
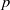 $p$-GROUPS
$p$-GROUPS
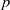 $p$-SUPERSOLUBLE GROUPS
$p$-SUPERSOLUBLE GROUPS