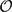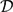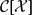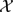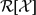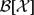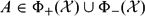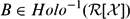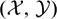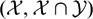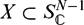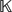Contents
Research Article
SOME NEW EXAMPLES OF SMASH-NILPOTENT ALGEBRAIC CYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 623-634
-
- Article
-
- You have access
- Export citation
PERTURBATIONS FROM INDEFINITE SYMMETRIC ELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2017, pp. 635-648
-
- Article
-
- You have access
- Export citation
ON CONJUGACY CLASSES OF THE KLEIN SIMPLE GROUP IN CREMONA GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 395-400
-
- Article
-
- You have access
- Export citation
A TRACE FORMULA FOR HECKE OPERATORS ON VECTOR-VALUED MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 143-165
-
- Article
-
- You have access
- Export citation
ON SERRE MICROFIBRATIONS AND A LEMMA OF M. WEISS
-
- Published online by Cambridge University Press:
- 20 March 2017, pp. 649-657
-
- Article
-
- You have access
- Export citation
HOMOLOGICAL DIMENSIONS OF CROSSED PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 401-420
-
- Article
-
- You have access
- Export citation
BEREZIN–TOEPLITZ QUANTIZATION, HYPERKÄHLER MANIFOLDS, AND MULTISYMPLECTIC MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 167-187
-
- Article
-
- You have access
- Export citation
DUAL SPACE AND HYPERDIMENSION OF COMPACT HYPERGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 421-435
-
- Article
-
- You have access
- Export citation
ON THE HOMOGENIZED ENVELOPING ALGEBRA OF THE LIE ALGEBRA Sℓ(2,ℂ) II
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 189-219
-
- Article
-
- You have access
- Export citation
PERTURBATION OF BANACH SPACE OPERATORS WITH A COMPLEMENTED RANGE
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 659-671
-
- Article
-
- You have access
- Export citation
A TOPOLOGICAL VARIATION OF THE RECONSTRUCTION CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 221-235
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE SCHWARTZ SPACE IS WEAKLY AMENABLE
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 437-443
-
- Article
-
- You have access
- Export citation
GORENSTEIN MODULES AND GORENSTEIN MODEL STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2017, pp. 685-703
-
- Article
-
- You have access
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
-
- Article
-
- You have access
- Export citation
EQUIVALENCE OF MODELS FOR EQUIVARIANT (∞, 1)-CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 237-253
-
- Article
-
- You have access
- Export citation
ABELIAN IDEALS IN A COMPLEX SIMPLE LIE ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 255-264
-
- Article
-
- You have access
- Export citation
HALF-LIBERATED MANIFOLDS AND THEIR QUANTUM ISOMETRIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2016, pp. 463-492
-
- Article
-
- You have access
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
-
- Article
-
- You have access
- Export citation
SOME SPHERE THEOREMS FOR SUBMANIFOLDS WITH POSITIVE BIORTHOGONAL CURVATURE
-
- Published online by Cambridge University Press:
- 07 February 2017, pp. 717-728
-
- Article
-
- You have access
- Export citation