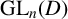Refine listing
Actions for selected content:
1419516 results in Open Access
Timing sensitivity of prenatal cortisol exposure and neurocognitive development
-
- Journal:
- Development and Psychopathology / Volume 37 / Issue 4 / October 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1707-1720
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Brun–Hooley sieve for 𝔽2[X] and squarefree shifts of integer polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1171-1195
-
- Article
- Export citation
ETS volume 44 issue 12 Cover and Front matter
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. f1-f2
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
Diversity of understory herbaceous plants during succession in rubber plantations in National Park of Hainan Tropical Rainforest, China
-
- Journal:
- Journal of Tropical Ecology / Volume 40 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e23
-
- Article
- Export citation
Insights into the synergistic effects of tectonics and climate from the formation and evolution of the Hongwen allochthonous deposit, southwestern China
-
- Journal:
- Quaternary Research / Volume 122 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 62-75
-
- Article
- Export citation
Marriage Unbound: State Law, Power, and Inequality in Contemporary China Ke Li. Stanford, CA: Stanford University Press, 2022. 344 pp. $30.00 (pbk), ISBN 9781503632011 - Decoupling: Gender Injustice in China's Divorce Courts Ethan Michelson. Cambridge and New York: Cambridge University Press, 2022. 521 pp. £29.99 (also available Open Access). ISBN 9781108738156
-
- Journal:
- The China Quarterly / Volume 260 / December 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1122-1124
- Print publication:
- December 2024
-
- Article
- Export citation
Associations between an energy-adjusted inflammatory diet index and incident depression: a cohort study
-
- Journal:
- British Journal of Nutrition , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-10
-
- Article
- Export citation
Metasurface loaded twin-port microstrip antenna with circular polarization features for UHF RFID applications
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 10 / December 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1798-1805
-
- Article
- Export citation
Ginkgo Village: Trauma and Transformation in Rural China Tamara Jacka. Canberra: ANU Press, 2024. 314 pp. AU$60.00 (also available Open Access). ISBN 9781760466411
-
- Journal:
- The China Quarterly / Volume 260 / December 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1120-1122
- Print publication:
- December 2024
-
- Article
- Export citation
Obesity and risk for liver disease: a two-sample Mendelian randomisation study
-
- Journal:
- British Journal of Nutrition / Volume 132 / Issue 10 / 28 November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1403-1410
- Print publication:
- 28 November 2024
-
- Article
- Export citation
Juliette Pattinson and Linsey Robb, eds. British Humour and the Second World War: “Keep Smiling Through” New Directions in Social and Cultural History. London: Bloomsbury Academic, 2023. Pp. 232. $115.00 (cloth).
-
- Journal:
- Journal of British Studies / Volume 63 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 961-963
-
- Article
- Export citation
LOCALLY NILPOTENT SUBGROUPS OF
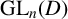 $\mathrm {GL}_n(D)$
$\mathrm {GL}_n(D)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 128-138
- Print publication:
- August 2025
-
- Article
- Export citation
Inter-row cover crops influencing the development of conilon coffee
-
- Journal:
- The Journal of Agricultural Science / Volume 162 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 236-244
-
- Article
- Export citation
Effective count of square-tiled surfaces with prescribed real and imaginary foliations in connected components of strata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 649-662
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Selection indexes in terms of functional features in modern dairy cattle breeding in Europe
-
- Journal:
- The Journal of Agricultural Science / Volume 162 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 260-267
-
- Article
-
- You have access
- HTML
- Export citation
Essential oils as a strategy to improve gut histomorphometry and performance of broilers: systematic review and meta-analysis
-
- Journal:
- The Journal of Agricultural Science / Volume 162 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 404-416
-
- Article
- Export citation
The Fate of Israel: Golda, directed by Guy Nattiv, Bleeker Street Media, 2023, 1 hr., 40 min.
-
- Journal:
- Nationalities Papers / Volume 53 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 496-497
-
- Article
- Export citation
The Belt Road and Beyond: State Mobilized Globalization in China, 1998–2018 Min Ye. Cambridge and New York: Cambridge University Press, 2020. 240 pp. £89.00; $105.00 (hbk). ISBN 9781108479561 - One Belt One Road: Chinese Power Meets the World Eyck Freymann. Cambridge, MA: Harvard University Asia Center, 2021. 439 pp. $28.00; £23.95 (pbk). ISBN 9780674247963
-
- Journal:
- The China Quarterly / Volume 260 / December 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1100-1102
- Print publication:
- December 2024
-
- Article
- Export citation
Least absolute shrinkage and selection operator regression used to select important features when predicting wheat yield from various genotype groups
-
- Journal:
- The Journal of Agricultural Science / Volume 162 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 245-259
-
- Article
- Export citation
Smooth and proper maps with respect to a fibration
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 9 / October 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 971-984
-
- Article
-
- You have access
- Open access
- HTML
- Export citation