Snails and freshwater fish were examined from four ponds in the Meinung township in which Clonorchis sinensis was known to be endemic 18 years ago. No metacercariae were found in 478 Tilapia nilotica, whereas of 451 Ctenopharyngodon idellus examined, 16.2%, 3.3% and 0.9% were found to be infected with Haplorchis pumilio, H. taichui and Clonorchis sinensis, respectively. In addition, there were some unidentified metacercariae in 12.0% of Ctenopharyngodon idellus examined. Overall, no positive correlation between infection rates and sizes of infected fish was shown. Six species of snails were collected in this survey and two frequently-occurring snails, Melanoides tuberculata and Thiara granifera were commonly infected with H. pumilio. Reasons for the prevalence of Haplorchis species and the absence of Clonorchis sinensis in fish and snail hosts in a previously reported endemic area for human clonorchiasis are discussed.

Previous literature attempted to gain insight into financial abuse involving people with dementia by analysing court cases, but these studies were limited in sample size or scope. This study collected 214 court rulings directly related to the financial decisions of people with dementia to identify characteristics of the financial abuse victim, perpetrators and the types of assets. The models of bystander intervention and routine activity theory were used as conceptual models to guide analysis regarding the role of bank staff as well as the court's decision in cases of financial abuse. The majority of financial abuse perpetrators were family members (73.8%), as opposed to outsiders (19.2%). Transfer of real estate was the most common legal issue, and land was the most common financial asset involved. Difficult intra-family relationships seem to pose a great risk of financial abuse involving people with dementia since adult children were found to be the most likely perpetrators (52.7%) but also plaintiffs accusing financial abuse (57.6%). In accordance with the bystander intervention model, bank staff were more likely to be suspicious of financial abuse when an outsider was regarded as the perpetrator. In accordance with the routine activity theory model, the court was more likely to acknowledge the case as an invalid financial decision when an outsider was regarded as the perpetrator in financial abuse cases. Since people with dementia suffer from greater losses due to their family members, future policies should establish guidelines for front-line bank staff to identify warning signs to reduce the risk of financial abuse involving people with dementia, not only to prevent fraud by outsiders but also exploitation by family members.

We study the effect of the Coriolis force on centrifugal buoyancy-driven convection in a rotating cylindrical shell with inner cold wall and outer hot wall. This is done by performing direct numerical simulations for increasing inverse Rossby number 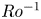$Ro^{-1}$ from zero (no Coriolis force) to 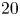$20$ (very large Coriolis force) and for Rayleigh number 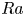$Ra$ from 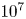$10^{7}$ to 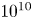$10^{10}$ and Prandtl number $Pr = 0.7$, corresponding to air. We invoke the thin-shell limit, which neglects the curvature and radial variations of the centripetal acceleration. As 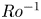$Ro^{-1}$ increases from zero, the system forms an azimuthal bidirectional wind that reaches its maximum momentum at an optimal 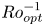$Ro^{-1}_{opt}$, associated with a maximal skin-friction coefficient $C_f$ and a minimal Nusselt number 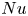$Nu$. Just beyond 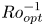$Ro^{-1}_{opt}$, the wind weakens and an axial, quasi-two-dimensional cyclone, corotating with the system, begins to form. A local ‘turbulence’ inverse Rossby number (non-dimensionalised by the eddy turnover time) determines the onset of cyclone formation for all 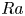$Ra$, when its value reaches approximately 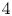$4$. At 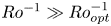$Ro^{-1} \gg Ro^{-1}_{opt}$, the system falls into the geostrophic regime with a sudden drop in 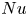$Nu$. The bidirectional wind for 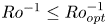$Ro^{-1} \le Ro^{-1}_{opt}$ is a feature of this system, as it hastens the boundary layer transition from laminar to turbulent, towards the ultimate regime. We see the onset of this transition at 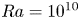$Ra=10^{10}$ and 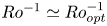$Ro^{-1}\simeq Ro^{-1}_{opt}$, although the mean flow profile has not yet fully collapsed on the Prandtl–von Kármán (logarithmic) law.

Highly turbulent Taylor–Couette flow with spanwise-varying roughness is investigated experimentally and numerically (direct numerical simulations with an immersed boundary method) to determine the effects of the spacing and spanwise width $s$ of the spanwise-varying roughness on the total drag and on the flow structures. We apply sandgrain roughness, in the form of alternating rough and smooth bands to the inner cylinder. Numerically, the Taylor number is $O(10^{9})$ and the roughness width is varied in the range $0.47\leqslant \tilde{s}=s/d\leqslant 1.23$, where $d$ is the gap width. Experimentally, we explore $Ta=O(10^{12})$ and $0.61\leqslant \tilde{s}\leqslant 3.74$. For both approaches the radius ratio is fixed at $\unicode[STIX]{x1D702}=r_{i}/r_{o}=0.716$, with $r_{i}$ and $r_{o}$ the radius of the inner and outer cylinder respectively. We present how the global transport properties and the local flow structures depend on the boundary conditions set by the roughness spacing $\tilde{s}$. Both numerically and experimentally, we find a maximum in the angular momentum transport as a function of $\tilde{s}$. This can be attributed to the re-arrangement of the large-scale structures triggered by the presence of the rough stripes, leading to correspondingly large-scale turbulent vortices.

We herein report an experimental study to explore the effects of impact inertia, film thickness and viscosity on the dynamics of shape deformation of a drop impacting a liquid film. We have identified that the spreading dynamics shows a weak dependence on impact inertia, but strongly depends on the film thickness. For a thick film, the liquid surface deforms and absorbs part of the impact energy, and hence inhibits spreading of the drop. For a thin film, the drop motion is restricted by the bottom solid substrate, promoting spreading. The periodicity of the capillary controlled shape oscillation, on the other hand, is found to be independent of impact inertia and film thickness. The damping of the shape oscillation shows strong dependence on the film thickness, in that the oscillation decays faster for smaller film thicknesses, due to the enhanced viscous loss.

Er doped ZnO (Er:ZnO) thin films with Er concentration from 0.1 to 3.6 at. % were prepared by dual beam ion beam sputter deposition at room temperature. Experimental results show that as Er concentration increases from 0.1 to 1.1 at. %, the resistivity of the as-deposited Er:ZnO film decreases from 560 Ω·cm to a minimum of 0.23 Ω·cm, while further increasing Er concentration to 3.6 at. % results in increase of the resistivity to 4.2 kΩ·cm. The as-deposited Er:ZnO with Er concentration of 1.1 at.% also exhibits the highest carrier concentration of 2.3×1019 cm-3. None of the as-deposited Er:ZnO films show 1.5 μm emission without post-growth annealing. Er:ZnO film with Er concentration at 0.5~1.1 at.% shows the strongest 1.5 μm emission after annealing at 700 ~ 900°C, while all the Er:ZnO film becomes semi-insulating after annealing. The discrepancy between the processing conditions for optimized carrier concentration and optimized optically activated Er ions may due to the formation of the pseudo-octahedral structure after annealing that favors the 1.5 μm emission.

Fluorescent nanodiamonds (FNDs) with a size in the range of 10 – 100 nm have been produced by ion irradiation and annealing, and isolated by differential centrifugation. Single particle spectroscopic characterization with confocal fluorescence microscopy and fluorescence correlation spectroscopy indicates that they are photostable and useful as an alternative to far-red fluorescent proteins for bioimaging applications. We demonstrate the application by performing in vivo imaging of bare and bioconjugated FND particles (100 nm in diameter) in C. elegans and zebrafishes and exploring the interactions between this novel nanomaterial and the model organisms. Our results indicate that FNDs can be delivered to the embryos of both organisms by microinjection and eventually into the hatched larvae in the next generation. No deleterious effects have been observed for the carbon-based nanoparticles in vivo. The high fluorescence brightness, excellent photostability, and nontoxic nature of the nanomaterial have allowed long-term imaging and tracking of embryogenesis in the organisms.

In the current research, we successfully prepared TiO2/Ni–Cu–Zn ferrite composite powder for magnetic photocatalyst. The core Ni–Cu–Zn ferrite powder was synthesized using the steel pickling liquor and the waste solution of electroplating as the starting materials. The shell TiO2 nanocrystal was prepared by sol-gel hydrolysis precipitation of titanium isopropoxide [Ti(OC3H7)4] on the Ni–Cu–Zn ferrite powder followed by heat treatment. From transmission electron microscopy (TEM) image, the thickness of the titania shell was found to be approximately 5 nm. The core of Ni–Cu–Zn ferrite is spherical or elliptical shape, and the particle size of the core is in the range of 70–110 nm. The magnetic Ni–Cu–Zn ferrite nanopowder is uniformly encapsulated in a titania layer forming core-shell structure of TiO2/Ni–Cu–Zn ferrite powder. The degradation efficiency for methylene blue (MB) increases with magnetic photocatalyst (TiO2/Ni–Cu–Zn ferrite powder) content. When the magnetic photocatalyst content is 0.40 g in 150 mL of MB, the photocatalytic activity reached the largest value. With a further increase in the content of magnetic photocatalyst, the degradation efficiency slightly decreased. This occurs because the ultraviolet (UV) illumination is covered by catalysts, which were suspended in the methylene blue solution and resulted in the inhibition in the photocatalytic reaction. The photocatalytic degradation result for the relationship between MB concentration and illumination revealed a pseudo first-order kinetic model of the degradation with the limiting rate constant of 1.717 mg/L·min and equilibrium adsorption constant 0.0627 L/mg. Furthermore, the Langmuir–Hinshelwood model can be used to describe the degradation reaction, which suggests that the rate-determining step is surface reaction rather than adsorption is in photocatalytic degradation.

ZnO thin films have been prepared by thermal oxidation of metal zinc films with different porosity. High and low porosity metal zinc films are prepared by DC magnetron sputtering and capillaritron ion beam sputtering, respectively. Near bandgap UV emission of ZnO thin films prepared from thermal oxidation of the low porosity film exhibit a maximum PL intensity after thermal oxidation at 410°C, while ZnO films prepared by thermal oxidation of the high porosity films exhibit a maximum PL intensity at oxidation temperature of 900°C. SEM micrographs indicate that ZnO prepared by thermal oxidation of low porosity films have a smooth surface morphology after thermal oxidation at 410°C, while ZnO prepared by thermal oxidation of high porosity zinc films exhibit a grain size of ∼ 800 nm after thermal oxidation at 1000°C.

Schwannoma arising from the tympanic membrane is a rare neoplasm. This report describes an external ear canal mass obscuring the tympanic membrane. A transcanal approach identified a tumour adhered to the tympanic membrane. The tumour was excised without myringoplasty. Pathology confirmed the diagnosis of schwannoma. Clinical examination revealed no evidence of recurrence during a follow-up period of one year. The possible origins of schwannoma of the tympanic membrane and lesion management are also discussed.

We have demonstrated organic thin-film transistor devices on synthesis paper of polypropylene (PP). All the fabrications are in solution-based processes except electrodes. As a barrier and smoother layer, photosensitive epoxy, 5μm-thich was coated on the paper substrate by using slit die coating. Polyvinyl phenol (PVP) was mixed with poly (melamine-co-formaldehyde) methylated, filmed by spin coating and ultraviolet (UV) cross linked to provide the gate dielectric layer. Using poly (3-hexylthiophene) as an active layer, a high-performance organic transistor with field effect mobility up to 0.006 cm2/ V s and an on/off ratio of 50 can be achieved. For the applications in flexible and disposable electronics, to built organic transistors on a cheap synthesis paper substrate can extremely lower the cost.

We found out the promising catalyst materials(NiPd). The NiPd not only has the low melting point but also has the Pd enhancing the surface diffusion at low temperatures(<500'c ). With the Pd film thickness increasing, we could control the CNT density and synthesize more aligned and uniform CNTs. We also obtained the better electrical properties including lower turn-on field (3.4 V/um) and higher current density (34.3 mA/cm2) for NiPd as catalyst. For the advantages described above, we believe that the difficulty of low temperature on FED can be overcome. Further, the large area field emission display might be fabricated in the future.

Measurement of electromigration parameters in the lead-free solder SnAg3.5 was carried out by utilizing U-groove solder lines and atomic force microscopy in the temperature range of 100–150 °C. The drift velocity was measured, and the threshold current densities of the SnAg3.5 solder were estimated to be 4.4 × 104 A/cm2 at 100 °C, 3.3 × 104 A/cm2 at 125 °C, and 5.7 × 103 A/cm2 at 150 °C. These values represent the maximum current densities that the SnAg3.5 solder can carry without electromigration damage at the three stressing temperatures. The critical products for the SnAg3.5 solder were estimated to be 462 A/cm at 100 °C, 346 A/cm at 125 °C, and 60 A/cm at 150 °C. In addition, the electromigration activation energy was determined to be 0.55 eV in the temperature range of 100–150 °C. These values are very fundamental for current carrying capability and mean-time-to-failure measurement for solder bumps. This technique enables the direct measurement of electromigration parameters of solder materials.

This work examines the interesting phenomenon of the generation of harmonics by non-breaking waves over permeable submerged obstacles. Nine model geometries, each with six different porosities, from 0.421 to 0.912, were considered to examine the effects of model width, porosity, and submergence depth on harmonic generation. The results revealed coupled effects on harmonic generation. A modified Ursell number was proposed to analyze experimental data. Almost no harmonic generation occurs at a modified Ursell number of less than five and/or a model width to wavelength ratio of over 1.6. After harmonics have been generated, wave profiles become dimpled, and the energy of the fundamental mode is transferred to higher-frequency components. Furthermore, the higher harmonics become more pronounced as the models widen, the depth of submergence becomes shallower, and model porosity declines.

The general approximate solutions for the two-dimensional thermoelastic problems with a nearly circular hole are provided in this study. Based on Stroh formalism and the method of conformal mapping, the boundary perturbation analysis is applied to solve the problems of a hole with arbitrary shape. The radius of the hole considered here is represented as a sum of a reference constant and a perturbation magnitude that is expanded into a Fourier series. In order to illustrate the applicability and efficiency of the present approach, special examples associated with polygonal hole problems are solved explicitly and discussed in detail. Since the general solutions have not been found in the literature, comparison is made with some special cases for which the analytical solutions exist, which shows that our proposed method is effective and general.

This study elucidated the complicated phenomena of wave refraction and diffraction around a circular island due to random incident waves traveling with a current. Various combinations of random incident wave and current conditions were used to investigate the wave height distributions around a circular island numerically and experimentally. Numerical calculations were carried out based on the theory derived by Lin & Hsu [1]. According to the results, it shows that numerical calculations can predict experimental data quantitatively well.

The thermoelastic problem associated with a point heat source embedded in an anisotropic body containing an elliptic hole or a rigid inclusion is considered in this paper. By using the formalism of Stroh [1], the approach of analytic function continuation and the technique of conformal mapping, the expression for the temperature, displacements and stress functions is expressed in explicit matrix form. The present derived solutions are also valid for some special problems such as a crack or a rigid line inclusion if one lets the minor axis of the ellipse approach to zero. The stress intensity factors induced by a point heat source are also obtained.

The electrical characteristics of thin gate dielectrics prepared by low temperature (850 °C) two-step N20 nitridation (LTN) process are presented. The gate oxides were grown by wet oxidation at 800 °C and then annealed in N2O at 850 °C. The oxide with N2O anneal, even for low temperature (850 °C), had nitrogen incorporation at oxide/silicon interface. The charge trapping phenomena and interface-state generation (ΔDitm) induced by constant current stressing were reduced and charge-to-breakdown (Qbd) under constant current stressing was increased. This LTN oxynitride was used as gate dielectric for N-channel MOSFET, whose hot-canrier immunity was shown improved and reverse short channel effect (RSCE) was suppressed.