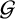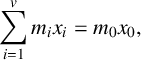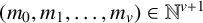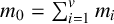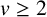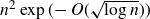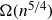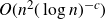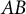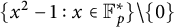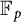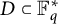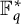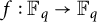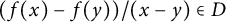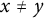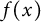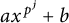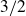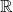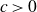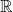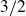Refine search
Actions for selected content:
71 results
Pointwise convergence of bilinear polynomial averages over the primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIMENSIONS OF SETS AVOIDING APPROXIMATE NONTRIVIAL ZEROS OF LINEAR PATTERNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-12
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
A non-flag arithmetic regularity lemma and counting lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 02 July 2025, pp. 635-679
- Print publication:
- March 2025
-
- Article
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finding product sets in some classes of amenable groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Restricted sumsets in multiplicative subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A strengthening of McConnel’s theorem on permutations over finite fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 213-218
- Print publication:
- March 2025
-
- Article
- Export citation
Simplices in large sets and directional expansion in ergodic actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial progressions in topological fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersective sets for sparse sets of integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1370-1402
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A better than
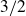 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 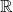 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 11-22
- Print publication:
- July 2024
-
- Article
- Export citation
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation