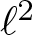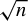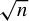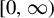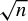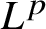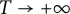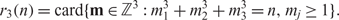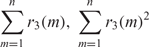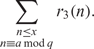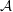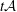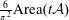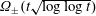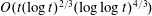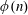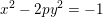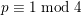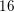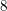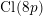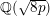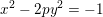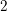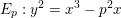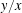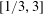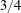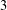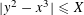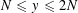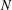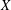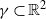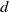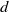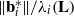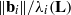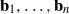Refine search
Actions for selected content:
16 results
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 218-246
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
Distribution and moments of the error term in the lattice point counting problem for three-dimensional Cygan–Korányi balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 830-861
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational points on nonlinear horocycles and pigeonhole statistics for the fractional parts of
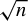 $\sqrt {n}$
$\sqrt {n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 3108-3130
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 21 April 2020, pp. 223-244
- Print publication:
- January 2021
-
- Article
- Export citation
Primitive Points in Rational Polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 850-870
- Print publication:
- December 2020
-
- Article
- Export citation
Spins of prime ideals and the negative Pell equation
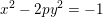 $x^{2}-2py^{2}=-1$
$x^{2}-2py^{2}=-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 100-125
- Print publication:
- January 2019
-
- Article
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
THE NUMBER OF SOLUTIONS TO MORDELL’S EQUATION IN CONSTRAINED RANGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 708-718
- Print publication:
- September 2015
-
- Article
- Export citation
THE TILED CIRCLE PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 321-346
- Print publication:
- July 2014
-
- Article
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
- Print publication:
- January 2014
-
- Article
- Export citation
SLIDE REDUCTION, SUCCESSIVE MINIMA AND SEVERAL APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 390-406
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF INTEGER LATTICE POINTS IN A BALL CENTRED AT A DIOPHANTINE POINT
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 118-134
- Print publication:
- January 2010
-
- Article
- Export citation