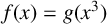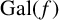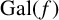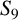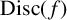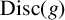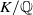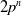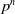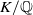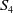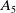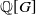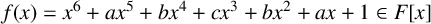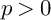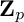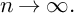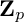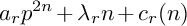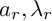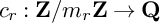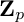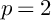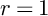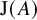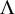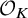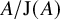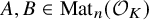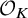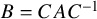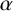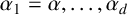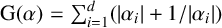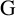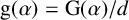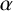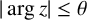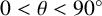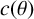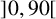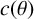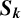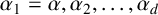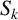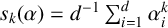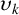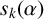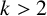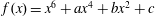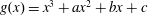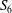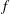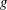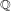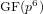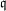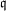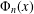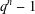Refine search
Actions for selected content:
34 results
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-15
-
- Article
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 460-467
- Print publication:
- December 2024
-
- Article
- Export citation
Leopoldt-type theorems for non-abelian extensions of
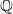 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 37-44
- Print publication:
- February 2024
-
- Article
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computation of lattice isomorphisms and the integral matrix similarity problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
- Print publication:
- April 2023
-
- Article
- Export citation
THE ABSOLUTE
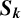 $\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
- Print publication:
- April 2023
-
- Article
- Export citation
ISOGENIES OF ABELIAN VARIETIES IN CRYPTOGRAPHY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 March 2020, pp. 508-509
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Galois Groups of Even Sextic Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 670-676
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Picard curves over
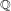 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
Explicit isogenies in quadratic time in any characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 267-282
-
- Article
-
- You have access
- Export citation
Reducing number field defining polynomials: an application to class group computations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 315-331
-
- Article
-
- You have access
- Export citation
Collecting relations for the number field sieve in
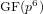 $\text{GF}(p^{6})$
$\text{GF}(p^{6})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 332-350
-
- Article
-
- You have access
- Export citation
ALGORITHMS FOR GALOIS GROUP COMPUTATIONS OVER MULTIVARIATE FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 169-170
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
PRIMITIVE PRIME DIVISORS AND THE
 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2015, pp. 122-135
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation